El triángulo de Pascal
Pautas en el triángulo
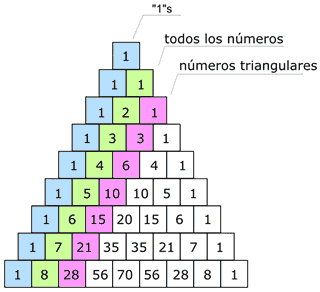 |
DiagonalesLa primera diagonal es, claro, sólo "unos", y la siguiente son todos los números consecutivamente (1,2,3, etc.)La tercera diagonal son los números triangulares (La cuarta diagonal, que no hemos remarcado, son los números tetraédricos.) | |||
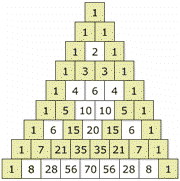
Pares e imparesSi usas distintos colores para los números pares e impares, obtienes un patrón igual al del Triángulo de Sierpinski |
 | |||
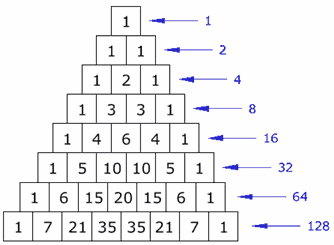 |
Sumas horizontales¿Notas algo en las sumas horizontales? ¿Hay algún patrón? ¡Es increíble!Se dobla cada vez (son las potencias de 2). | |||
| ||||
| ||||
Usar el triángulo de Pascal
Caras y cruces
El triángulo de Pascal te dice cuántas combinaciones de caras y cruces de pueden salir tirando monedas. Así puedes averiguar la "probabilidad" de cualquier combinación.Por ejemplo, si tiras una moneda tres veces, sólo hay una manera de sacar tres caras (CCC), pero hay tres maneras de sacar dos caras y una cruz (CCX, CXC, XCC), también tres de sacar una cara y dos cruces (CXX, XCX, CXX) y sólo una de sacar tres cruces (XXX). Esta es la pauta "1,3,3,1" en el triángulo de Pascal.
| Tiradas | Resultados posibles (agrupados) | Triángulo de Pascal |
|---|---|---|
| 1 | H T |
1, 1 |
| 2 | HH HT TH TT |
1, 2, 1 |
| 3 | HHH HHT, HTH, THH HTT, THT, TTH TTT |
1, 3, 3, 1 |
| 4 | HHHH HHHT, HHTH, HTHH, THHH HHTT, HTHT, HTTH, THHT, THTH, TTHH HTTT, THTT, TTHT, TTTH TTTT |
1, 4, 6, 4, 1 |
| ... etc ... |
| ¿Cuál es la probabilidad de sacar exactamente dos caras con 4
monedas? Hay 1+4+6+4+1 = 16 (o 4×4=16) resultados posibles, y 6 de ellos dan exactamente dos caras. Así que la probabilidad es 6/16, o 37.5% |
Combinaciones
El triángulo también muestra cuántas combinaciones de objetos son posibles.Por ejemplo, si tienes 16 bolas de billar, ¿de cuántas maneras puedes elegir tres de ellas (sin hacer diferencia del orden en que las eliges)?
Respuesta: baja a la fila 16 (la primera es la fila 0), y mira 3 lugares a la derecha, allí está la respuesta, 560. Aquí tienes un trozo del triángulo en la fila 16:
1 14 91 364 ... 1 15 105 455 1365 ... 1 16 120 560 1820 4368 ...
Polinomios
El triángulo de Pascal también te da los coeficientes en la expansión de un binomio:| Potencia | Expansión polinomial | Triángulo de Pascal |
|---|---|---|
| 2 | (x + 1)2 = 1x2 + 2x + 1 | 1, 2, 1 |
| 3 | (x + 1)3 = 1x3 + 3x2 + 3x + 1 | 1, 3, 3, 1 |
| 4 | (x + 1)4 = 1x4 + 4x3 + 6x2 + 4x + 1 | 1, 4, 6, 4, 1 |
| ... etc ... |
Las 15 primeras líneas
Como referencia, aquí tienes las filas 0 a 14 del triángulo de Pascal 1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
1 9 36 84 126 126 84 36 9 1
1 10 45 120 210 252 210 120 45 10 1
1 11 55 165 330 462 462 330 165 55 11 1
1 12 66 220 495 792 924 792 495 220 66 12 1
1 13 78 286 715 1287 1716 1716 1287 715 286 78 13 1
1 14 91 364 1001 2002 3003 3432 3003 2002 1001 364 91 14 1
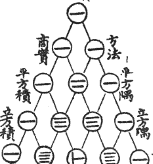 |
Los chinos ya lo conocíanEste dibujo se titula "El antiguo gráfico del método de los siete cuadrados multiplicadores". Ver imagen completaEsto es de la portada del libro de Chu Shi-Chieh "Ssu Yuan Yü Chien" (Espejo precioso de los cuatro elementos), escrito en 1303 (¡hace más de 700 años!), y en el libro se dice que el triángulo ya era conocido más de dos siglos antes. |
El quincunce
 |
Esta asombrosa máquina creada por Sir Francis Galton es un
triángulo de Pascal hecho con palos. Se llama quincunce. Las bolas se dejan caer sobre el primer palo y rebotan hasta abajo del triángulo donde caen en pequeños contenedores.
|
Otras curiosas propiedades del Triángulo de Pascal
El Triángulo de Pascal debe su nombre al filósofo y matemático Blaise Pascal (1623-1662). Sin embargo, como en muchos casos matemáticos, su origen es muy anterior. Se tienen referencias que datan del siglo XII en China. De hecho, algunas de sus propiedades ya fueron estudiadas por el matemático chino Yang Hui (siglo XIII), así como el persa Omar Khayyam (siglo XII).
Recordemos brevemente su construscción. El triángulo se construye desde la cúspide hacia abajo. El primer elemento es el número 1, formando la fila 0. La fila 1 está formada por dos elementos, ambos también el número 1. A partir de aquí, la construcción es como sigue: cada fila está formada por un elemento más que la anterior. El elemento primero y último de cada una siempre será el número 1, y cada elemento interior será el número resultado de sumar los dos elementos que se sitúan encima de él y adyacentes en la fila superior.

Veamos algunas curiosidades:
Desarrollo de potencias de binomios
La fórmula general del llamado Binomio de Newton está formada por unos coeficientes que coinciden con los elementos de la fila cuyo número de orden es la potencia a la que está elevado el binomio. La fórmula general, recordemos, es:
Los coeficientes K1, K2 ,K3 ... coinciden con los números de la fila n del triángulo de Pascal.
Números combinatorios
Los números del triángulo de Pascal coinciden con los números combinatorios. El número combinatorio Cn,m representa el número de grupos distintos de m elementos que se pueden formar a partir de n objetos, de forma que cada grupo se diferencie de otro en algún elemento (combinaciones de n elementos tomados de m en m). En nuestra construcción, n representa la fila del elemento y m su lugar dentro de ella. Así, se le puede dar el carácter de fórmula general para saber, sin necesidad de construir todas las filas anteriores, cuál es el número que ocupa un lugar determinado, a la de los números combinatorios:
Números poligonales
Los números poligonales fueron descubiertos/inventados por los pitagóricos. Podemos disponer los números enteros formando figuras geométricas, por ejemplo 3 guijarros se pueden disponer formando un triángulo, 4 forman un cuadrado, etc. Así los pitagóricos construyeron:
Los números triangulares (1, 3, 6, 10, 15, ...) son enteros del tipo N = 1 + 2 + 3 + ... + n
Los números cuadrados (1, 4, 9, 16, 25, ...) son enteros del tipo N = 1 + 3 + 5 + 7 + ... + (2n-1)
Los números pentagonales (1, 5, 12, 22, ...) son enteros del tipo N = 1 + 4 + 7 + ... +(3n-2)
Los números hexagonales (1, 6, 15, 28, ...) son enteros del tipo N = 1 + 5 + 9 + ... + (4n-3)
Y así sucesivamente.

En general, los números poligonales son enteros del tipo  .
.
Para b=1 tenemos números triangulares, para b=2 cuadrados, para b=3 pentagonales.
Observemos que en el triángulo de Pascal, los números triangulares se encuentran en la diagonal que empieza en uno de los extremos de la fila tercera: 1,3,6,10...

Los números cuadrados se encuentran en el triángulo de Pascal recurriendo a la misma diagonal que en el caso anterior: construimos cada uno sumando dos números triangulares consecutivos. Eso nos proporciona: 1, 4, 9, 16, 25, ...

De hecho, por este método recurrente podemos construir todos los números poligonales, y en ese sentido están presentes en el triángulo de Pascal.
Según conjeturó Fermat, todo número entero puede expresarse mediante la suma de n números n-gonales como máximo. Esta conjetura fue demostrada para los números triangulares y cuadrados por Gauss, mientras que Cauchy consiguió dar finalmente una demostración general.
El "stick de hockey"
Cualquier diagonal que empiece en un extremo del triángulo, y de la longitud que sea, cumple la siguiente propiedad: La suma de todos los números que la integran se encuentran justo debajo del último de ellos, en la diagonal contraria. Con este dibujo se entenderá mejor:

Potencias de 11
Esta propiedad es un poco más esotérica. Podemos interpretar cada fila como un único número. Si la fila está formada por números de un solo dígito, basta unirlos. En el caso de la fila 2 tenemos:
1-2-1 ............................ 121 = 112
Cuando los números de la fila constan de más de un dígito, se "reparten" para formar el número final como se observa en el ejemplo siguiente para la fila 5:
1-5-10-10-5-1 ........... 1-(5+1)-(0+1)-0-5-1=1-6-1-0-5-1 ............ 161051 = 115
Números primos
Si el primer elemento de una fila es un número primo, todos los números de esa fila serán divisibles por él (menos el 1, claro). Así, en la fila 7: (1 7 21 35 35 21 7 1), los números 7,21 y 35 son divisibles por 7.
Suma de las filas
La suma de los elementos de cualquier fila es el resultado de elevar 2 al número que define a esa fila. Así:
20 = 1
21 = 1+1 = 2
22 = 1+2+1 = 4
23 = 1+3+3+1 = 8
24 = 1+4+6+4+1 = 16
21 = 1+1 = 2
22 = 1+2+1 = 4
23 = 1+3+3+1 = 8
24 = 1+4+6+4+1 = 16
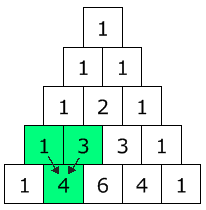
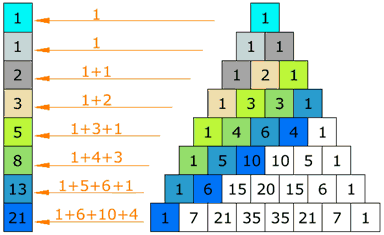
Sucesión de Fibonacci
La serie de Fibonacci puede ser encontrada también en el triángulo de Pascal. Dividiendo al mismo según las líneas que mostramos en el diagrama, los números atrapados entre ellas suman cada uno de los elementos de esta sucesión. Recordemos que esta sucesión (que, por cierto, se construye de manera similar al triángulo de Pascal), es: 1,1,2,3,5,8,13,21,... (an+1 = an + an-1 con a0 = 1, a1 = 1)

AQUÍ TE DEJAMOS UNOS LINKS, PARA QUE AMPLIES TU CONOCIMIENTO. RECUERDA QUE EL CONOCIMIENTO ES PODER
Cibergrafía:


No hay comentarios:
Publicar un comentario