8 DE AGOSTO/2014
PARADOJAS
El término paradoja viene del griego (para y doxos) y significa más allá de lo creíble. En la actualidad la palabra paradoja tiene numerosos significados:
- Afirmación que parece falsa, aunque en realidad es verdadera.
- Afirmación que parece verdadera, pero en realidad es falsa.
- Cadena de razonamientos aparentemente impecables, que conducen sin embargo a contradicciones lógicas. (Las paradojas de esta clase suelen llamarse falacias.)
- Declaración cuya veracidad o falsedad es indecible.
- Verdad que se vuelve patas arriba para llamar la atención.
LAS PARADOJAS DE ZENÓN
- El movimiento es imposible
- Aquiles no alcaza a la tortuga
DOS PADRES Y DOS HIJOS
Dos padres y dos hijos se van de viaje, suben al coche, pero si observamos atentamente a la llegada sólo bajan tres personas y no queda nadie dentro ¿Es posible?
¿SÓLO UN 1%?
Una sandía fresca tiene 10 kg de masa, de la que el 99% es agua. Partimos la sandía y la dejamos al sol sin darnos cuenta de que se nos puede secar, comprobamos posteriormente que la proporción de agua sólo es del 98 %. ¿Cuánto pesa ahora la sandía?
GEOGRAFÍA
- Una persona se ha comprado una casa de planta cuadrada con una ventana en cada una de las cuatro paredes y de modo que todas las ventanas den al sur ¿Es posible?
- Una persona sale de paseo en dirección norte y camina 2000m, gira hacia el este y camina otros 2000 m y por último gira hacia el sur y camina otros 2000 m ¿Es posible que haya llegado ya al punto de partida?
Un ganadero dejó al morir 11 vacas que debían repartirse entre sus tres hijos de modo que el mayor recibiera la mitad, el segundo la cuarta parte y el tercero la sexta parte. Mientras los hijos discutían sobre como hacer el reparto para que no hubiera que derramar mucha sangre de vaca, un vecino enterado del tema se acerco con una de sus vacas y les dijo: “os presto esta vaca para que podáis repartir mejor”. Efectivamente se repartieron la mitad(6), la cuarta(3) y la sexta parte(2) de las doce sin usar violencia alguna y comprobaron que después quedaba una vaca que tranquilamente se volvió a llevar el vecino ¿Cómo es posible?
Inés ha salido en bicicleta para subir a una cima que se encuentra a 10 km de su casa. Como es cuesta arriba sólo ha podido sacar un promedio de 10 km/h . ¿A qué velocidad debe bajar para que le salga un promedio 25 km/h en la totalidad del paseo?
¿QUIÉN TIENE RAZÓN?
Está cerca el final de curso y pronto vendrán las interpretaciones de los datos, en los que cada uno suele buscar la perspectiva más favorable a sus intereses (solemos hacerlo todos, basta recordar las declaraciones de los distintos líderes políticos después de conocerse los resultados de las elecciones: todos parecen haber ganado)
Nosotros nos vamos a fijar en una situación próxima: los resultados obtenidos al acabar 3º de bto en un Instituto en dos años seguidos, en los cuales hemos distinguido según que los alumnos fueran repetidores o hicieran 3º por primera vez. Los datos aparecen en la siguiente tabla:
2013
|
2014
| |||
MATRICULADOS
|
APROBADOS
|
MATRICULADOS
|
APROBADOS
| |
NO REPETIDORES
|
22
|
12
|
15
|
8
|
REPETIDORES
|
3
|
3
|
10
|
9
|
TOTAL
|
25
|
15
|
25
|
17
|
Hasta aquí los datos. Los mismos para todos. Lo que difieren son las interpretaciones. He aquí algunas:
El director: “ El año 2013 marca un avance del 13 % en el número de aprobados entre nuestro alumnado de 3º. Es una buena demostración del buen trabajo que han realizado a lo largo del año nuestro profesorado y alumnos y alumnas. Les felicito a todos por ello”
Un profesor del centro: “Le agradezco al director su comentario, pero no hay que lanzar las campanas al vuelo, puesto que la tasa de aprobados no ha crecido más que un 8%”
Un alumno de 3º: “Como siempre los profesores miran las cosas de una forma extraña. Se sea repetidor o no este año las cosas han ido peor para los alumnos. No creo que sea cosa de felicitaciones”
Un alumno repetidor: “Tampoco creo que sea para ponerse como dice el compañero, porque la verdad es que repitiendo este año tenía un 35´5 % más de posibilidades de aprobar que el curso pasado”
Otro alumno repetidor: “Desde luego que no. Este año repitiendo, tenías un 10% menos de posibilidades que en el 2013”
Es evidente que los comentarios no sólo difieren algo, sino que parecen absolutamente contradictorios. Analízalos y decide quién o quiénes, de todos ellos, tienen razón.
UN ENUNCIADO Y SU CONTRARIO
(No siempre que un enunciado es falso su contrario es verdadero)
Esta frase consta de siete palabras Es claramente un enunciado falso, ya que consta de seis palabras. Por tanto, su contrario debería ser verdadero. ¿Es esto correcto?
¡Es falso! La oración contraria: Esta frase no consta de siete palabras. está formada exactamente por siete palabras. ¿Cómo resolver estos raros dilemas?
LOS TRES ENUNCIADOS FALSOS.
Tenemos aquí tres enunciados falsos. ¿Serías capaz de descubrirlos?
a) 2 + 2 = 4 b) 3 x 6 =17 c) 8/4 = 2
d) 13 – 6 = 5 e) 5 + 4 = 9
UNA DE LAS DOS.
He aquí dos afirmaciones. Una de ellas es falsa. ¿Cuál?
La primera es cierta: hay dos afirmaciones, ella misma y la segunda. Si la segunda fuese falsa, ella misma habría de decir que no hay ninguna falsa (al ser falsa) y si fuese verdadera, ¿dónde está la falsa? Por lo que nos introducimos en una clara contradicción.
PARADOJA DEL MENTIROSO
Ésta es, sin duda, una de las paradojas más famosas que se conocen. Se atribuye al cretense Epiménides haber hecho la siguiente afirmación:
Todos los cretenses son mentirosos.
Una versión simplificada de la paradoja del mentiroso es la siguiente:
Esta frase es falsa.
Se puede ver claramente que esta frase contiene la paradoja del mentiroso. La diferencia aquí es que esta frase se refiere a ella misma mientras que Epiménides lo hace indirectamente.
Relacionados con estas paradojas hay numerosos problemas relativos a cierta isla en la que habitaban “caballeros” que siempre decían la verdad y “escuderos” que siempre mentían. Os propongo los siguientes:
A. Tres de los habitantes de la isla A, B y C están en la calle y un extranjero que pasaba por allí le preguntó a A: “¿Eres caballero o escudero?”, A respondió pero el extranjero no entendió bien la respuesta, entonces preguntó a B: “¿Qué ha dicho?” y B le respondió: “A ha dicho que es escudero” y el tercer hombre C puntualizó: “No creas a B, está mintiendo”. La pregunta es: ¿Qué son B y C?
B. Hay ahora sólo dos individuos A y B, y A le dice a B “Uno al menos de nosotros es escudero” ¿Qué son A Y B?
C. Vuelven a estar tres: A, B y C, se oye a A decir:”Los tres somos escuderos”. En cambio B dice: “Uno y sólo uno de nosotros es caballero”. ¿Qué son A, B y C?
PARADOJA DE NEWCOMB
El nombre de esta paradoja se debe a su inventor, el físico William Newcomb. Es una curiosa paradoja que consiste en:
Un científico dispone de un equipo muy sofisticado capaz de estudiar la mente humana. Con la información proporcionada por dicho equipo puede predecir con mucha exactitud cómo decidiría una persona cualquiera frente a una disyuntiva.
Este científico sometió a prueba a muchas personas. La prueba consistía en dos cajas: una caja A, transparente, que contenía 100000 pesetas, y otra caja B, opaca, que bien podía estar vacía, bien podía contener 100 millones de pesetas.Este científico le decía a sus sujetos:
Tiene usted dos opciones:
A. Una es tomar ambas cajas y quedarse con su contenido
B. Tomar solamente la caja B y quedarse con su contenido. Ahora bien, si usted decide llevarse las dos cajas, yo lo habría previsto con mi equipo y entonces habría dejado vacía la caja B, con lo que usted se llevaría solamente 1000 euros. Sin embargo, si usted decide llevarse solamente la caja B, también lo hubiera previsto, y hubiera dejado ahí 1 millón de euros, por lo que usted se los llevaría. Mi equipo ya ha previsto cómo reaccionará usted, y yo ya he determinado si dejar en la caja B el millón o no.
Las reacciones pueden ser:
A. Ya he visto al científico realizar muchos experimentos, y en todos ellos su predicción fue correcta. Los que cogieron las dos cajas se llevaron solamente 1000 euros. Por tanto, me llevaré la caja B, y así ganaré 1 millón de euros.
B. Este científico ya ha hecho su predicción, y ya no va a cambiar el contenido de la caja B. Si está vacía, seguirá vacía, y si está llena, seguirá llena. Por tanto, me llevaré las dos, y me quedaré todo lo que tengan.
A la vista de esta paradoja, surge la pregunta: ¿Quién de los dos tomó mejor decisión?. No es posible que ambos razonamientos sean correctos. Por tanto, ¿cuál es erróneo, y por qué?.
Esta paradoja cuestiona si el futuro está completamente determinado o no.
PARADOJA DE RUSSELL
Relacionada con esta cuestión está la paradoja de Russell basada en la definición de conjunto. La mencionaremos brevemente. Podemos definir cualquier conjunto mediante una propiedad, los elementos que la verifican pertenecen a él y los que no la verifican no pertenecen. Pero ¿y si definimos el conjunto A de los conjuntos que no se contienen a si mismos? ¿Contendrá a A?.
Una versión de esta paradoja, algo más sencilla, es la paradoja del barbero: «el barbero de esta ciudad, que afeita sólo a todos los hombres que no se afeitan a sí mismos, ¿se afeita a sí mismo?»
PARADOJA DEL QUIJOTE
Aparece en el capítulo LI del libro segundo del Quijote, se cuenta que, para entrar a la isla había un guardia que a preguntaba a cada visitante para qué iba a la isla. Si respondía con verdad, el guardia le dejaba pasar y no había ningún tipo de problema. Sin embargo, si el visitante respondía con mentira, era ahorcado. Un día llegó un visitante y a la pregunta respondió:
He venido aquí para ser ahorcado
Los guardias quedaron confusos, pues no sabían qué debían hacer.
- Si el visitante decía la verdad, debían dejarle pasar. Pero puesto que dijo la verdad, debía ser ahorcado, pues si no, habría mentido.
- Si el visitante había mentido, debían ahorcarle. Como había mentido, no podía ser ahorcado, pues si no, habría dicho la verdad y debían dejarle pasar a la isla.
Los guardias consultaron al gobernador de la isla y decidió ser clemente, ya que, hiciera lo que hiciera, quebrantaría la ley. Y dejó en libertad al visitante.
Agosto 18/2014
TRECE PARADOJAS
Por norma general, ante muchas situaciones, acostumbramos dejarnos llevar por
el sentido común y la lógica, que son las
mismas que nos dictan los parámetros para pensar y decidir en base a un
determinado escenario.
Sin embargo, en ciertas ocasiones, las cosas terminan siendo muy diferentes a
lo que pensabamos en un principio, o directamente, desafían el sentido común y
la lógica, llegando al punto de resultar imposibles. A este
concepto se le denomina paradoja.
Veamos un listado de 13 paradojas muy curiosas e
interesantes, algunas de ellas bastante conocidas:
1. El gato de Schrödinger

Una de mis paradojas preferidas es la del experimento
teórico de El gato de Schrödinger. Pertenece al campo
de la física, más concretamente al de la física
cuántica.
En el experimento de Schrödinger, tenemos una caja
totalmente opaca, con 3 elementos en su interior: un gato
(vivo), una botella con un gas venenoso y un aparato
con una partícula radioactiva, la cual tiene una probabilidad
del 50% de desintegrarse.
En el caso de desintegrarse, la botella libera el gas, matando al gato. En el
caso de no desintegrarse, no ocurre absolutamente nada (y el gato
vive).
La paradoja consiste en que, según nuestro sentido común, el gato estará vivo
o muerto pero no podremos saberlo hasta abrir la caja. Según las leyes de la
física cuántica, el gato está vivo y muerto
(los dos estados a la vez) hasta que se abra la caja y se
compruebe.
En el mundo de Internet es muy conocida (quizás por el mero hecho de
existir un gato en la demostración) y ha llegado hasta el punto de tener su
propio Schrödinger Nyan
cat [*].
Existe una variación del gato de Schrödinger, denominado El
suicidio cuántico, aunque también podríamos denominarlo la venganza
del gato de Schrödinger, ya que se desarrolla la teoría desde el punto
de vista del gato (y con un humano).
Youtube | El gato de
Schrödinger
2. El cuadrado perdido
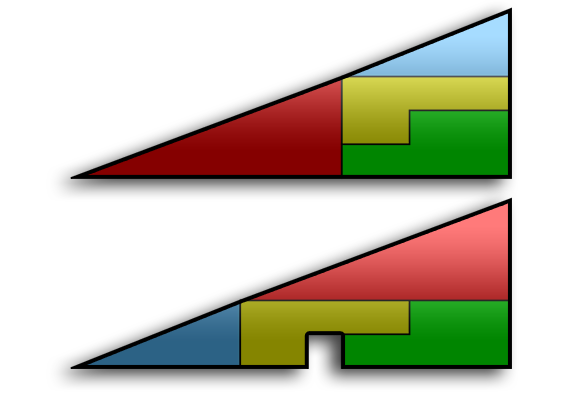
El problema del cuadrado perdido es una paradoja muy conocida y utilizada en el inicio del estudio de la geometría, dentro del campo de las matemáticas.
La paradoja consiste en la reordenación de los elementos del triángulo de la
imagen superior. ¿Cómo es posible que sólo reordenando las
mismas piezas, nos sobre ese espacio cuadrado?
Obviamente, tiene truco y se trata sólo de una ilusión óptica. En los
siguientes enlaces se puede observar claramente la explicación de ese cuadrado
que desaparece.
Animación visual | El
cuadrado perdido
3. La cinta de Möbius
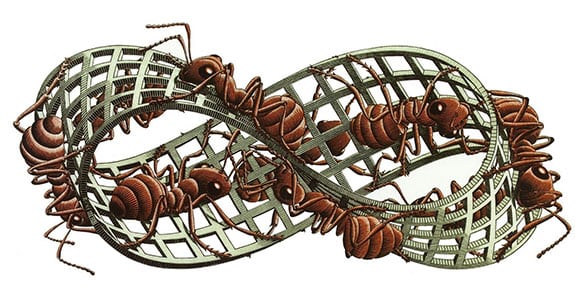
La banda o cinta de Möbius (o Moebius) es una
figura simple y muy sencilla de construir que se utiliza mucho en el ámbito de
las matemáticas (geometría) o en
topología.
Entre las propiedades de esta cinta, que son las que la hacen paradójica,
quizás la que más destaca es que tiene una sola cara y
un solo borde, lo que lo convierte en algo similar a un
objeto imposible (pero obviamente, posible), al puro
estilo de M.
C. Escher, de hecho, la imagen superior es de su autoría.
Youtube | Construir una
banda de Möbius
4. La paradoja del abuelo

La paradoja del abuelo es una paradoja física muy utilizada
en la ciencia ficción, ya que tiene su base en los viajes en el tiempo. Es muy
conocida y se ha utilizado en muchas obras, como por ejemplo
Terminator, Regreso al futuro o
Futurama.
Suponiendo el caso de que una persona pudiera viajar hacia atrás en el
tiempo, retrocediera varios años y matase a su abuelo antes de
que tuviera descendencia (concretamente al padre del viajero del
tiempo), este no habría nacido ni hubiera tenido hijos,
por lo cual el viajero del tiempo tampoco nacería ni le sería posible viajar en
el tiempo para matar a su abuelo.
Es curioso como se han ideado ciertas soluciones a esta paradoja para hacer
posible el suceso, como la existencia de universos paralelos,
líneas temporales alternativas o tantas otras. Otra paradoja
relacionada con la ciencia ficción, es la
paradoja de Fermi.
5. ¿El huevo o la gallina?

Probablemente, la paradoja más conocida del mundo.
«¿Qué ocurrió primero, la gallina o el
huevo?». En el caso de ser la gallina, se plantea que la gallina tuvo
que salir de un huevo. En el caso de ser el huevo, éste lo tuvo que poner una
gallina.
Este dilema, adjudicado a las ramas de la filosofía, es muy
conocido en la cultura popular y se han realizado multitud de teorías sobre
ella. Por ejemplo, Aristóteles afirmaba que lo primero en
existir fue la gallina, mientras que Stephen Hawking asegura
que lo fue el huevo.
6. La paradoja del cumpleaños
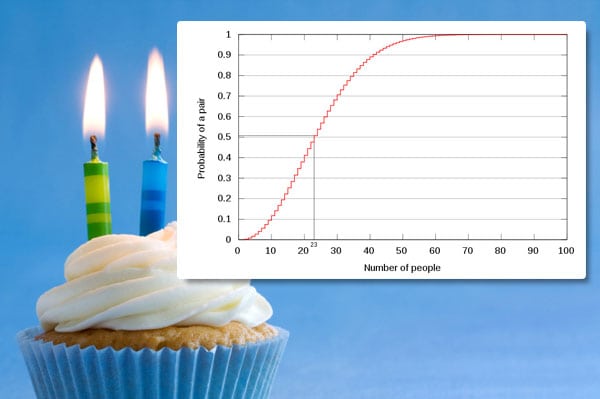
Esta paradoja, pertenece al campo de las matemáticas, más específicamente a la estadística.
Se dice que en un cumpleaños con 23 personas, existe una probabilidad de más
del 50% de que al menos dos personas cumplan años el mismo día. De hecho, si hay
50 personas, la probabilidad es casi del 100% (97%
exactamente).
Esta paradoja sorprende mucho por una especie de ilusión
mental, ya que el sentido común dicta lo contrario que la demostración
matemática. Aún así, si no te crees la paradoja, puedes comprobarlo en el
simulador visual del enlace.
7. El teorema de los infinitos monos

Otro teorema clásico y popular, que quizás no llega a ser paradoja, pero sí
merece la pena añadir en este listado, es el teorema de los
infinitos monos. Es tan conocido que ha sido referenciado en multitud de
obras, desde el libro La guia del autoestopista galactico, de
Douglas Adams, hasta en varios capítulos de Los Simpsons, entre
muchos otros.
El teorema afirma que si un número infinito de monos
escribieran a máquina por un intervalo infinito de tiempo,
acabarían escribiendo las obras de Shakespeare.
Aunque el teorema original versaba sobre un sólo mono y
cualquier libro de la Biblioteca Nacional Francesa, la cultura
popular hizo que se popularizara esta versión. Hace varios años, también se
llevó a cabo un experimento (Experimento Vivaria)
donde tomaron fotos y realizaron pruebas a varios monos, para ver que eran
capaces de escribir y durante cuanto tiempo.
Más información | Infinite monkey
theory
8. La paradoja de Monty Hall

Otra paradoja perteneciente al campo de la estadística es la paradoja de Monty Hall, también llamada la paradoja de las tres puertas.
En un concurso televisivo tenemos tres puertas cerradas.
Detrás de una de ellas hay un coche, mientras que detrás de las
otras dos, hay una cabra respectivamente.
Después de que el concursante haga su elección (y antes de comprobar si
ha acertado), el presentador abre una de las puertas no
elegidas donde sabe que hay una cabra y le pregunta al concursante
«¿Está seguro de querer abrir esa puerta o quiere elegir otra?»
El sentido común dicta que no hay diferencia entre cambiar o no la elección
de la puerta, sin embargo, el problema tiene trampa, ya que si nos quedamos con
la puerta elegida inicialmente tenemos menos probabilidades de
acierto que si cambiamos de puerta.
Simulador | Monty Hall
Simulator
9. La paradoja de Abilene

La paradoja de Abilene es una situación estudiada en el campo de la sociología en la que un grupo de personas realizan una acción que no quieren realizar (individualmente) porque ningún miembro está dispuesto a objetar algo o negarse.
En una calurosa tarde, un matrimonio y su suegra están jugando al dominó a la
sombra. El suegro propone hacer un viaje a Abilene (un caluroso viaje de más
de 80km). La mujer acepta «¡Gran idea!». El marido dice «A mi me parece
bien, espero que a tu madre también». «Por supuesto», responde.
Tras realizar el viaje, con más horas de lo previsto, malhumorados y
agotados, la suegra dice «Menudo viaje. Hubiera preferido quedarme en casa, pero
acepté porque estaban muy ilusionados». El marido reconoce que vino sólo para
satisfacer al resto ya que pensó que estarían aburridos, mientras que la mujer
sostiene que aceptó para no estropear el plan de los demás.
Finalmente, quedan perplejos. Decidieron en común hacer un viaje que ninguno
de ellos quería hacer.
Otros experimentos sociológicos similares, en los que puedes tomar parte,
podrían ser La
mujer y el puente o La princesa y el
toro.
10. La paradoja de los gemelos

La paradoja de los gemelos (o de los relojes) es un experimento teórico catalogado dentro de la física (relatividad).
Dos gemelos deciden realizar un experimento: Uno de ellos
viajará en una nave a la velocidad de la luz a una estrella,
mientras que el otro se queda en la Tierra.
De acuerdo con la dilatación del tiempo (teoría de la relatividad),
cuando el gemelo viajero vuelva a la Tierra, será más joven que el que se quedó,
ya que el tiempo del gemelo de la nave va más despacio que el de la
Tierra.
Youtube | Paradoja de
los gemelos
Más información | Twin
Paradox
11. El dilema del prisionero

El dilema del prisionero no es una paradoja en sí, pero es un problema dentro de la rama de la teoría de juegos que puede considerarse paradójico.
La policía arresta a dos sospechosos. No hay pruebas suficientes para
condenarlos, sin embargo, se les separa en dos celdas
diferentes y se les ofrece el mismo trato: Si uno de ellos
confiesa y su cómplice no, se condenará 10 años al cómplice y se liberará al
delator. Si ambos confiesan, se condenarán a 6 años cada uno. Si ninguno
confiesa, sólo podrán encerrarlos durante 6 meses por cargos menores.
El experimento muestra que dos personas no cooperarán,
incluso aunque en ello vaya el interés de las dos.
Es curioso saber que, en una variación de este problema, el
prisionero iterado, se repite varias veces el mismo juego, añadiendo la
posibilidad de castigar al otro jugador por la no cooperación
en partidas previas. El incentivo para defraudar termina siendo superado por la
amenaza del castigo, por lo que conduce a una cooperación forzada.
12. La paradoja del hotel infinito

El Hotel infinito de Hilbert es una metáfora paradójica relacionada con el mundo de las matemáticas.
Dos grandes empresarios con un hotel gigante, tienen el problema de que
quieren garantizar a los clientes que siempre tendrán una habitación disponible
para un nuevo cliente. Como el hotel actual, con 1.000.000 de habitaciones no
era suficiente, tomaron cartas en el asunto.
Los dos empresarios decidieron construir el primer hotel con habitaciones
infinitas. Un número infinito de habitaciones garantizaba dar alojamiento a un
número infinito de clientes. Pero al llegar un nuevo cliente, se vieron de nuevo
con el mismo problema.
Para ello idearon una solución. Dar alojamiento a los clientes con la única
condición de que si llega un nuevo cliente, tienen que abandonar su habitación e
irse a la habitación siguiente (+1). Así, el nuevo cliente se
hospedaría en la habitación 1, y el resto se iría rodando a la habitación
directamente siguiente. Como el hotel tiene un número infinito de habitaciones,
no habría última habitación.
Más información | El Gran Hotel
Cantor
13. La paradoja de la serpiente

Finalmente, para terminar, otra paradoja popular, muy similar al de el huevo o la gallina, denominada La paradoja de la serpiente, muy utilizada en campos y materias de filosofía.
Un uróboro es una palabra griega que representa a un animal
que engulle su propia cola, formando un círculo. Si dicho animal, por ejemplo,
una serpiente, comienza a comerse su cola y termina tragándose todo su cuerpo...
¿Dónde estaría la serpiente?
La paradoja entra en juego cuando nos damos cuenta que la serpiente se
encuentra dentro de su propio estómago, pero simultáneamente sigue comiéndose a
sí misma.
Fuente: http://www.emezeta.com/tag/logica

No hay comentarios:
Publicar un comentario