TEOREMA DE PITAGORAS Y DE THALES

Última actualización 9 de Febrero/2015

CONTENIDO DE LA PÁGINA

1. Teorema dePitágoras
2. Ejerccios resueltos del teorema de Pitágoras
3. Repsando el teorema  de Pitágoras
4. Teorema de Thales
5. Aplicaciones del teorema de Pitágoras
6. Pitagoras mucho más que un teorema (Vídeo)
7. Áplicaciones del teorema d Pitágoras (Vídeo)

VÍDEO: PITÁGORAS MAS QUE UN TEOREMA
VÍDEO: APLICACIONES DEL TEOREMA DE PITÁGORAS

TEOREMA DE PITÁGORAS Y APLICACIONES

Hace años, un hombre llamado Pitágoras descubrió un hecho asombroso sobre triángulos: Si el triángulo tiene un ángulo recto (90°)... ... y pones un cuadrado sobre cada uno de sus lados, entonces... ... ¡el cuadrado más grande tiene exactamente la misma área que los otros dos cuadrados juntos!

El lado más largo del triángulo se llama "hipotenusa", así que la definición formal es:

En un triángulo rectángulo el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los otros dos lados (llamamos "triángulo rectángulo" a un triángulo con un ángulo recto)

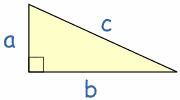Entonces, el cuadrado de a (a²) más el cuadrado de b (b²) es igual al cuadrado de c (c²): a2 + b2 = c2

¿Seguro... ?

Veamos si funciona con un ejemplo. Un triángulo de lados "3,4,5" tiene un ángulo recto, así que la fórmula debería funcionar.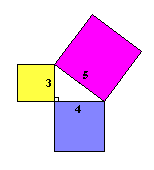

Veamos si las áreas son la misma: 32 + 42 = 52 Calculando obtenemos: 9 + 16 = 25 ¡sí, funciona!

De acuerdo con esto podemos afirmar que:

En un triángulo rectángulo el cuadrado construido sobre  la hipotenusa es igual a la suma de los cuadrados cosntruidos sobre los catetos

¿Por qué es útil esto?

Si sabemos las longitudes de dos lados de un triángulo con un ángulo recto, el Teorema de Pitágoras nos ayuda a encontrar la longitud del tercer lado. (¡Pero recuerda que sólo funciona en triángulos rectángulos!)

Escríbelo como una ecuación:

a2 + b2 = c2

Ahora puedes usar álgebra para encontrar el valor que falta, como en estos ejemplos:

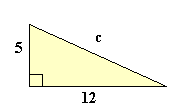a2 + b2 = c2 52 + 122 = c2 25 + 144 = 169 c2 = 169 c = √169 c = 13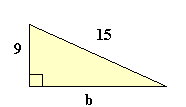

a2 + b2 = c2 92 + b2 = 152 81 + b2 = 225 Resta 81 a ambos lados b2 = 144 b = √144 b = 12

¡Y Puedes Demostrarlo Tú Mismo!

Consigue papel y tijeras, y usa la siguiente animación como guía:

Dibuja un triángulo rectángulo en el papel, dejando mucho espacio alrededor. Dibuja un cuadrado sobre la hipotenusa (el lado más largo) Dibuja un cuadrado del mismo tamaño en el otro lado de la hipotenusa Dibuja líneas como la que se muestra, así: Recorta los trozos Colócalos de manera que puedas demostrar que el cuadrado grande tiene la misma área que los cuadrados en los otros lados juntos El tema es apasionante, porque muchos cálculos de la vida cotidiana pueden plantearse como problemas resueltos aplicando Teorema de Pitágoras. Como he señalado antes, el reto es interpretar la letra del enunciado, en lo posible hacer un dibujo o croquis sencillo de la misma y buscar la forma de definir algún triángulo rectángulo, del que se conozcan dos lados y se quiera calcular el otro. Este tipo de situaciones es diferente a las que hemos visto antes, donde en un principio sólo se trató de Resolución de triángulos con Teorema de Pitágoras y como paso siguiente algo más complejo como los Ejercicios resueltos Teorema de Pitágoras. Estos problemas tienen una letra, tú debes interpretarla, elaborando el dibujo y resolver el enigma. Veamos los ejemplos de… EJERCICIOS RESUELTOS calcular la hipotenusa de los siguientes triángulos 1.

2. 

3. 

4.

5. 

Calcular el cateto incógnita

6. 

7.

8. Dada la figura calcular la mediada incógnita

.

Los siguientes problemas tienen una letra, tú debes interpretarla, elaborando el dibujo y resolver el enigma. Veamos los ejemplos de…

Problemas resueltos aplicando Teorema de Pitágoras

1. Una ciudad se encuentra 17 km al oeste y 8 km al norte de otra. ¿Cuál es la distancia real lineal entre las dos ciudades?
2. Una escalera cuya longitud es de 3 metros  se encuentra apoyada contra una pared en el suelo horizontal y alcanza 2,8 m sobre esa pared vertical. La pregunta es: ¿a qué distancia está al pie de la escalera de la base de la pared?
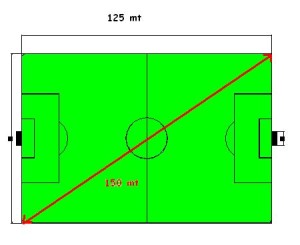
3. Una cáncha de fútbol (rectangular como sabemos)  mide 125 metros de largo. Si la longitud de sus diagonales es de 150 metros. ¿cuál es el ancho del campo de juego?

Soluciones

1) Lo primero es realizar un pequeño dibujo que nos permita identificar la situación y ver cómo definimos un triángulo rectángulo en la misma.

Este podría ser un buen dibujo, donde observamos que se cumplen los datos que nos da el problema y que además la distancia real entre las ciudades, vendría a ser la hipotenusa de nuestro triángulo rectángulo.

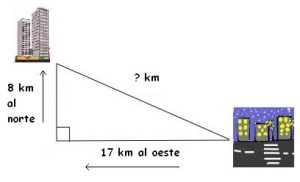El triángulo entonces queda claramente definido y sabemos que tenemos un cateto que mide 17 km, otro que mide 8 km y que la distancia real que se nos está pidiendo es la hipotenusa del tal triángulo. Aplicamos Teorema de Pitágoras y el planteo sería así:

a² = b² + c²
a² = 8² + 17² = 64 + 289 = 353
 a = √353 = 18.8
Respuesta final: la distancia real entre las dos ciudades es de 18,8 km
2)

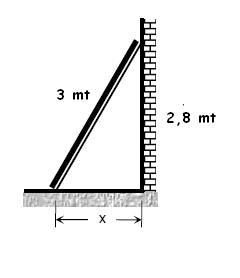En este caso, el dibujo que podemos hacer para interpretar la letra del problema sería algo como esto, donde nuevamente se identifica sin problemas el triángulo rectángulo.

Queda claro que la escalera cumple el rol de la hipotenusa, la altura de la pared (dato conocido) es uno de los catetos y la distancia del pie de la escalera hasta la base de la pared, es el otro cateto, precisamente la medida que se nos pide calcular y que como es una incógnita para nosotros hemos llamado “x”.

El planteo de resolución en este caso podría ser el siguiente:
a² = b² + c²
3² = b² + 2.8²
 9 =  b² + 7.84
b² = 9 – 7.84 = 1.16
b = √1.16 = 1.08
Respuesta final: el pie de la escalera está a 1,08 mt de la pared.
3) Primer paso: la figura que ayuda a comprender

 Analizando la figura, vemos que el triángulo queda comprendido por esa diagonal del campo de juego (la hipotenusa), el largo del campo (uno de los catetos) y el ancho (el otro cateto cuya longitud es  lo que se nos pide hallar).

 El planteo de resolución sería el siguiente:

 a²         =  b² + c²
150²     = 125² + c²
22,500  = 15,625 + c²
         c² = 22,500 – 15,625 = 6,875
         c  = √6,875
          c = 82.9
Respuesta final: el ancho del campo de fútbol es de 82,9 metros

REPASANDO EL TEOREMA DE PITÁGORAS

Si estás a punto de rendir un examen sobre este tema, esta es tu oportunidad de poder comprobar cuánto sabes sobre Teorema de Pitágoras.

Para empezar puedo remitirte a algunos post anteriores en los que aprendimos todo acerca del Teorema de Pitágoras, e incluso hicimos los tres niveles de aplicaciones clásicas en relación a este tema (resolver triángulos con datos, resolver ejercicios y resolver problemas).

He aquí los links a esos post anteriores, ordenados de más simple a más complejo por si recién tomas contacto con el tema o por si tu intención es hacer un repaso pautado del mismo.

• Teorema de Pitágoras      (incluye un video muy claro con algo de historia y aplicaciones del Teorema de Pitágoras. Recomendado)
• Resolución de triángulos con Teorema de Pitágoras
• Ejercicios resueltos Teorema de Pitágoras
• Problemas resueltos aplicando Teorema de Pitágoras
• Pitágoras y trigonometría para resolver triángulos rectángulos

Todos estos últimos post, cuentan con propuestas de ejercicios y se aportan sus resultados de tal modo que puedas tú mismo ir resolviendo y comparando.

Te invito a tomarte un tiempo y leer detenidamente cada uno de los post a la vez que realizas paso a paso los ejercicios. Cuando te sientas listo ahora sí podrás realizar este test dinámico que te devolverá al finalizar el resultado y comprobarás por ti mismo…

1.

 b=35

 b=5

 b=√ 377

 b=√ 135

Question 1 of 6

2.

 a=5

 a= √ 527

 a=25

 a=31

TEOREMA DE THALES

El filósofo y matemático griego Tales de Mileto fue uno de los siete sabios más grandes de la antiguedad.

El teorema de Tales, llamado así en su memoria, es una parte fundamental en  el estudio de la semejanza. A él se debe una de las numerosas aplicaciones que tiene la semejanza, que es la determinación de la distancia entre dos puntos inaccesibles entre sí; para ello se dice que calculó la altura de una de las pirámides de Egipto sin medirla directamente, basándose en la longitud de la sombra de su bastón; así logró realizar una brillante triangulación



El teorema de Tales afirma:´

Si tres o más paralelas son cortadas por transversales, la razón entre las medidas de dos segmentos cualesquiera cortados por una transversal será igual a la razón de las medidas de los segmentos correspondientes de la otra, es decir, son proporcionales.

Al trazar el ángulo TOS y dividir la recta OT en tres segmentos en donde cada división se marca con los puntos P, Q y R, si se trazan paralelas que corten a OT y OS por lo puntos P, Q y R, se originan los puntos U, V, W.
 

En la figura las medidas de los segmentos son las siguientes:

OP=2cm; PQ=2.5cm; QR=3cm
OU=3cm; UV=3.75cm; V W=4.5cm

Al establecer proporciones con las medidas, se observa que:

 es decir que las medidas de los segmentos correspondientes, son proporcionales.

En esta otra figura, al medir los segmentos MN, MN' NP y NP', se puede observar que las medidas son proporcionales:

al comprobar que los segmentos son proporcionales, se puede afirmar que las rectas NN' y PP' son paralelas. Así que:

Si una recta intriseca a dos lados de un triángulo, y los divide proporcionalmente, entonces la recta es paralela al tercer lado.

Como consecuencia del teorema de Tales, se puede enunciar el teorema fundamental de semejanza de triángulos.

Toda paralela a uno de los lados de un triángulo, divide a los otros dos en segmentos proporcionales, por lo que forman un triángulo semejante al primero.

Obsérvese el triángulo PQR, al trazar la recta TS paralela al lado RP se puede demostrar que:


 por tener los lados proporcionales y los {angulos homólogos congruentes.

RP II TS

El ángulo Q es común a los dos triángulos



Los triángulos PQR y SQT tienen ángulos congruentes.
Además:

por el teorema de Tales



Para obtener la proporcionalidad entre los segmentos, se traza la recta VS, paralela a RQ.
 Pero en el paralelogramo STRV, RV = TS. Se puede sustituir:
así que los lados de los triángulos PQR y SQT son proporcionales


Por lo tanto  porque sus ángulos correspondientes son congruentes y sus lados homólogos proporcionales. 


APLICACIONES DEL TEOREMA DE THALES


EJEMPLO 1

Sirve para calcular alturas de edificios teniendo referencias de otros elementos que si que nos es fácil medir, como por ejemplo un árbol y ayudándonos en los rayos del sol, las proyecciones de sobra.

Escribimos la proporción:

6  = 270

5       h       

(Siendo h la altura del edificio)

Y resolvemos la proporción:

6x = 270 * 5

 x = 1350

           6

x = 225

EJEMPLO 2

Aplicando el teorema de Tahles determine  el valor de lso segmentos AB y BC de la figura

AB = 2x – 3
BC = x + 2
A’B’ = 5
B’C’ = 6

Determinando o valor de x:

AB = 2x – 3 → 2*4 – 3 = 5
BC = x + 2 → 4 + 2 = 6



EJEMPLO 3

Determine el valor de x