ÚLTIMA ACTUALIZACIÓN 7 DE AGOSTO/2015
CONTENIDO DEL CURSO
LECCIÓN 1. POLINOMIOS
LECCIÓN 2. EXPONENTES
LECCIÓN 3. DEFINICIONES BÁSICAS
LECCIÓN 4. LEYES DE LOS EXPONENTES
LECCIÓN 5. EXPONENTES NEGATIVOS
LECCIÓN 6. EXPONENTES FRACCIONAROS
LECCIÓN 7. POLINOMIOS
LECCIÓN 8. COMO SE RESUELVE UNA ECUACIÓN
LECCIÓN 9. TEORIA DE ECUACIONES 1
LECCIÓN 10. TEORÍA DE ECUACIONES 2
LECCIÓN 11. TEORÍA DE ECUACIONES 3
LECCIÓN 12. TEORIA DE ECUACIONES DE SEGUNDO GRADO 1
LECCIÓN 13. TEORIA DE ECUACIONES DE SEGUNDO GRADO 2
LECCIÓN 14. TEORIA DE ECUACIONES DE SEGUNDO GRADO 3
LECCIÓN 15. TEORIA DE ECUACIONES DE SEGUNDO GRADO 4
LECCIÓN 16. TEORIA DE ECUACIONES DE SEGUNDO GRADO 5
LECCIÓN 16. TEORIA DE ECUACIONES DE SEGUNDO GRADO 5. para ir al link de clik sobre EL TÍTULO
LECCIÓN 15. TEORIA DE ECUACIONES DE SEGUNDO GRADO 4. para ir al link de clik sobre EL TÍTULO
LECCIÓN 14. TEORIA DE ECUACIONES DE SEGUNDO GRADO 3. para ir al link de clik sobre EL TÍTULO
LECCIÓN 13. TEORIA DE ECUACIONES DE SEGUNDO GRADO 2. para ir al link de clik sobre EL TÍTULO
LECCIÓN 12. TEORIA DE ECUACIONES DE SEGUNDO GRADO 1. para ir al link de clik sobre EL TÍTULO

LECCIÓN 11. TEORÍA DE ECUACIONES 3. para ir al link de clik sobre EL TÍTULO
LECCIÓN 10. TEORÍA DE ECUACIONES 2. para ir al link de clik sobre EL TÍTULO
LECCIÓN 9. TEORIA DE ECUACIONES DE PRIMER GRADO. para ir al link de clik sobre la imagen
LECCIÓN 8. COMO SE RESUELVE UNA ECUACIÓN
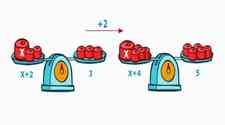
Para empezar a aprender cómo se resuelve una ecuación es necesario tener en claro qué es una ecuación. Una ecuación es una expresión en la que hay una o varias cantidades desconocidas llamadas incógnitas. Siempre tendrás un signo de =, indicando que los términos que están del lado derecho tienen el mismo valor que los términos del lado izquierdo. (Los términos son cada una de las cantidades de que están separados por un signo + o -). Las letras que aparezcan en la ecuación son las incógnitas, y para encontrar su valor debes seguir los pasos de cómo se resuelve una ecuación.
El valor de la incógnita, o variable, debe hacer cierta la ecuación, es decir, qué número debe sustituir a la para que la ecuación sea una expresión verdadera. En el ejemplo debes responder a la pregunta: ¿cuánto debe valer x para que sea cierto que multiplicando x por 2 y sumándole 1 sea 7?
2x+1=7
Sin hacer muchos cálculos se puede deducir que x vale 3:
2(3)+1=7
6+1=7
7=7
Antes de ahondar en el cómo se resuelve una ecuación es importante aclarar que para que se mantenga la relación de igualdad “lo que haces de un lado de la ecuación lo debes hacer el otro” es decir, si sumas, por ejemplo, un 3 al lado derecho, debes también sumar un 3 al lado izquierdo, si multiplicas por 5 el lado izquierdo, debes multiplicar por 5 el lado derecho también. De esta forma el valor del lado derecho sigue siendo el mismo que el del lado izquierdo. Mira:
5(2x+1)=5(7) → multiplicamos ambos lados por 3
10x+5=35
10(3)+5=35
30+5=21
21=21 → se sigue manteniendo la igualdad
Para saber cómo se resuelve una ecuación, el primer paso es dejar todos los términos que contienen la x del mismo lado y pasar el resto al otro. Pero no, no es tan simple como crees… para poder pasar un término a un lado o al otro del = pasas el término con la operación contraria, si se está sumando tú lo pasas restando, y al revés, si se está restando lo pasas sumando.

Después debes reducir los términos semejantes, (dos o más términos son semejantes cuando tienen la mima letra, afectada por el mismo exponente, y se reducen haciendo la operaciones indicadas, + →suma, – → resta). Mira el ejemplo:



Cuando ya tienes únicamente un término de cada lado lo único que falta, para aprender cómo se resuelve una ecuación, es despejar la variable. Posiblemente te preguntaras qué es despejar, pero no te preocupes, no es nada complejo, simplemente es dejar ‘solita’ la y para poder lograrlo aplicas el mismo principio que usamos para pasar los términos con a un solo lado: pasas al otro lado ‘todo lo que te estorbe’ con la operación contraria. En el ejemplo ‘nos estorba’ el 18, que está multiplicando a la x, entonces lo pasamos dividiendo al 3


Simplificas, y ¡listo! Has resuelto una ecuación

 y lo puedes comprobar sustituyendo en la ecuación
inicial.
y lo puedes comprobar sustituyendo en la ecuación
inicial.





Como puedes observar, en ambos lados de la ecuación ha resultado el mismo valor ;).
LECCIÓN 7. POLINOMIOS

LECCIÓN 8. COMO SE RESUELVE UNA ECUACIÓN
Para empezar a aprender cómo se resuelve una ecuación es necesario tener en claro qué es una ecuación. Una ecuación es una expresión en la que hay una o varias cantidades desconocidas llamadas incógnitas. Siempre tendrás un signo de =, indicando que los términos que están del lado derecho tienen el mismo valor que los términos del lado izquierdo. (Los términos son cada una de las cantidades de que están separados por un signo + o -). Las letras que aparezcan en la ecuación son las incógnitas, y para encontrar su valor debes seguir los pasos de cómo se resuelve una ecuación.

El valor de la incógnita, o variable, debe hacer cierta la ecuación, es decir, qué número debe sustituir a la para que la ecuación sea una expresión verdadera. En el ejemplo debes responder a la pregunta: ¿cuánto debe valer x para que sea cierto que multiplicando x por 2 y sumándole 1 sea 7?
2x+1=7
Sin hacer muchos cálculos se puede deducir que x vale 3:
2(3)+1=7
6+1=7
7=7
¿Cómo se resuelve una ecuación?
En ecuaciones sencillas como la del ejemplo no es muy difícil encontrar el valor de la incógnita sin gran uso de álgebra, pero ¿cómo se resuelve una ecuación más compleja?Antes de ahondar en el cómo se resuelve una ecuación es importante aclarar que para que se mantenga la relación de igualdad “lo que haces de un lado de la ecuación lo debes hacer el otro” es decir, si sumas, por ejemplo, un 3 al lado derecho, debes también sumar un 3 al lado izquierdo, si multiplicas por 5 el lado izquierdo, debes multiplicar por 5 el lado derecho también. De esta forma el valor del lado derecho sigue siendo el mismo que el del lado izquierdo. Mira:
5(2x+1)=5(7) → multiplicamos ambos lados por 3
10x+5=35
10(3)+5=35
30+5=21
21=21 → se sigue manteniendo la igualdad
Para saber cómo se resuelve una ecuación, el primer paso es dejar todos los términos que contienen la x del mismo lado y pasar el resto al otro. Pero no, no es tan simple como crees… para poder pasar un término a un lado o al otro del = pasas el término con la operación contraria, si se está sumando tú lo pasas restando, y al revés, si se está restando lo pasas sumando.
Después debes reducir los términos semejantes, (dos o más términos son semejantes cuando tienen la mima letra, afectada por el mismo exponente, y se reducen haciendo la operaciones indicadas, + →suma, – → resta). Mira el ejemplo:

Cuando ya tienes únicamente un término de cada lado lo único que falta, para aprender cómo se resuelve una ecuación, es despejar la variable. Posiblemente te preguntaras qué es despejar, pero no te preocupes, no es nada complejo, simplemente es dejar ‘solita’ la y para poder lograrlo aplicas el mismo principio que usamos para pasar los términos con a un solo lado: pasas al otro lado ‘todo lo que te estorbe’ con la operación contraria. En el ejemplo ‘nos estorba’ el 18, que está multiplicando a la x, entonces lo pasamos dividiendo al 3

Simplificas, y ¡listo! Has resuelto una ecuación
Comprobación
El valor de la incógnita que hace que la expresión sea cierta es



Como puedes observar, en ambos lados de la ecuación ha resultado el mismo valor ;).
Cómo resolver una ecuación, cómo resolverla, cómo proceder cuando te
enfrentas a una de ellas, es ni más ni menos el punto clave de la lección de
hoy. Comienzo por decirte que todo depende de la ecuación de la que estemos
hablando y para abordar el tema comenzaré con las ecuaciones más sencillas, vale
decir las ecuaciones lineales o de primer grado.
Toma nota y verás que es posible establecer una serie de pasos que serán aplicables a todos los casos que se te presenten en relación a…
Veamos un ejemplo sencillo
En este caso, sólo uno de los miembros de la
igualdad (el primero) es una expresión que contiene una variable. Resolver o
hacer una ecuación implica trabajar con ambos miembros de la igualdad, hasta
lograr despejar (aislar) a la variable en el primer miembro de la misma, es
decir llegar a una expresión de la forma x = …. (un valor).
En concreto ¿cuál es el método a aplicar si queremos resolver o hacer una ecuación? El truco es el siguiente: debes elegir convenientemente una operación que vaya dejando aislada a la x en el primer miembro de la igualdad y aplicarla siempre a los dos miembros de la igualdad. Este último punto es muy importante para sostener la igualdad.
Veamos un paso a paso para el ejemplo anterior:
Si restamos 1 en ambos miembros de la igualdad (es decir de los dos lados),
al operar anularíamos el +1 del primer miembro. Observa:
Si dividimos por 7 en ambos miembros de la igualdad (es decir de los dos
lados), al operar quedaría la x sola tal como la queríamos y podemos saber cuál
es el valor que buscábamos. Observa:
¿Es ésta la solución que
buscábamos? ¿Cómo sabemos si esta forma de resolver o hacer una ecuación nos ha
devuelto el valor correcto de x? Muy sencillo, además de hacer o resolver una
ecuación, tú debes verificar el resultado simplemente
escribiendo la expresión inicial, pero en vez de x escribes el valor que
hallaste, en este caso, 3. Si operas de los dos lados de la igualdad y obtienes
una igualdad evidente, será correcta la solución que hallaste. Observa:
Queda claro que el resultado ha sido correcto,
por lo que ahora sí, ya sabes cómo hacer una ecuación: el método es ir operando
de ambos lados de la igualdad de tal modo que en el primer miembro de la misma,
la x debe ir quedando aislada o despejada.
ECUACIONES CON FRACCIONES
Cómo resolver ecuaciones con fracciones es muy similar a cómo resolver ecuaciones con enteros, pero debes tener en cuenta una serie de reglas básicas que te permitirán manejar las fracciones sin miedo. Una ecuación es fraccionaria si al menos uno de sus términos tiene denominador, es decir, que tengas aunque sea una incógnita dividida entre un número.
Cómo resolver ecuaciones con fracciones se vuelve mucho más sencillo si suprimes los denominadores y la conviertes en una ecuación con enteros. Te podrás preguntar cómo se convierte esto, pero es muy sencillo: Lo primero que tienes que hacer para saber cómo resolver ecuaciones con fracciones es suprimir los denominadores, o sea encontrar el mínimo común múltiplo (m.c.m.) de todos los denominadores que tengas en tu ecuación. (El m.c.m. de dos o más expresiones algebraicas es la que tenga el coeficiente numérico más pequeño y el exponente menor, que se puede dividir exactamente entre cada una de las expresiones dadas) En el ejemplo de cómo resolver ecuaciones con
fracciones, el m.c.m. entre los denominadores (que son 2, 1 y 4) es 4 porque 4
se puede dividir exactamente entre 2, entre 1 y entre 4, mira
En el ejemplo de cómo resolver ecuaciones con
fracciones, el m.c.m. entre los denominadores (que son 2, 1 y 4) es 4 porque 4
se puede dividir exactamente entre 2, entre 1 y entre 4, mira  Ahora bien, una vez encontrado el m.c.m. de tu
expresión, lo que tienes que hacer para continuar en el cómo resolver ecuaciones
con fracciones es multiplicar toda la ecuación por ese número. (Recuerda que una
ecuación no se altera si haces las mismas
Ahora bien, una vez encontrado el m.c.m. de tu
expresión, lo que tienes que hacer para continuar en el cómo resolver ecuaciones
con fracciones es multiplicar toda la ecuación por ese número. (Recuerda que una
ecuación no se altera si haces las mismas
operaciones de los dos lados del signo igual.) Y listo, lo que sigue para saber cómo resolver
ecuaciones con fracciones es encontrar el valor de la incógnita de la misma
forma que resolverías
una ecuación con enteros: reduces términos semejantes, despejas la incógnita
y resuelves.
Y listo, lo que sigue para saber cómo resolver
ecuaciones con fracciones es encontrar el valor de la incógnita de la misma
forma que resolverías
una ecuación con enteros: reduces términos semejantes, despejas la incógnita
y resuelves. 
En caso de que te encuentres con un numerador con un polinomio (que tenga más de un término, o sea que tenga alguna suma o resta en la parte de arriba de la fraccion) no cambia nada en el cómo se resuelven ecuaciones con fracciones: se realizan los mismos pasos; ahora verás.
En el ejemplo puedes observar que todos los numeradores son más de un término, pero eso no afecta en nada, tu debes encontrar el m.c.m. de los denominadores: entre los números 1,5, 3 y 6 su m.c.m. es 30, así que multiplicamos toda la ecuación por 30
Y al eliminar todos los denominadores, entonces resolvemos la ecuación de la misma forma como se resuelve una con enteros: despejando la incógnita.

En estos dos ejemplos es muy sencillo saber cuál es el m.c.m., pero para el caso de que te encuentres con denominadores más complejos, te explico una manera sencilla de encontrar el m.c.m. de cualquier combinación de números, siempre y cuando sean monomios.



Por lo tanto el m.c.m. es
ECUACIONES CON RADICALES
Para resolver las Ecuaciones con Radicales, nos apoyamos en la siguiente propiedad: “Cualquier raíz de una ecuación dada, puede ser también raíz de otra ecuación que se obtenga al igualar los cuadrados de los dos miembros de la ecuación propuesta”, sin embargo, al elevar al cuadrado los dos miembros de una ecuación, se obtienen valores para la incógnita, que pueden resultar incorrectos para la ecuación original; estos valores se denominan, Raíces Extrañas de la Ecuación, esto sucede porque los radicales de índice con número par, presentan problemas de indefinición con sub radicales negativos.
1. Se deja en uno de los miembros un sólo radical, trasladando al otro miembro los demás términos.
2. Los mienbros de la ecuación obtenida se elevan al cuadrado, al cubo, etcétera, y se igualan entre sí dependiendo del índice de la raíz involucrada.
3. Si la ecuación que obtengas no contiene radicales la podemos resolver normalmente, si por el contrario, contiene uno o más radicales se repiten los pasos 1 y 2 hasta que obtengas una ecuación sin radicales, y luego resuelves esta última ecuación.
4. Ahora es necesario que sustituyas los valores obtenidos en el paso anterior, en la ecuación original y ya puedes determinar las raíces extrañas.
El proceso de liberar la ecuación de radicales lo conocemos con el nombre de racionalización de la ecuación.
En los siguientes ejemplos puedes encontrar diferentes formas de solucionar las ecuaciones con radicales:
Primer ejemplo:
√ (x + 3) = 4

Al sustituir x=13 en la ecuación original para revisar si es una raíz extraña o no, nos percatamos que =4, es correcta. Por tanto. S = {13 }.
Segundo ejemplo:
√(2x²-1) =x

Si sustituimos x= -1 en la ecuación original, obtenemos: √2(-1)²-1= (-1)
Podemos observar que el miembro derecho no puede ser negativo, es decir; =-1, por esta razón, descartamos -1 por ser una raíz extraña y ubicamos x=1, entonces tenemos S = {1}.
√(4.16-15)- 8 = -1
√(64-15)- 8 = -1
√(49)- 8 = -1
7-8=-1.
Esta solución es la correcta y se toma como: S = {4}.
Recuerda seguir practicando operaciones con números radicales, próximamente tendremos nuevos artículos con ejemplos y ejercicios sobre el tema para que puedas seguir profundizando tus conocimientos
Toma nota y verás que es posible establecer una serie de pasos que serán aplicables a todos los casos que se te presenten en relación a…
Cómo hacer una ecuación
Comienzo por recordarte una definición que ya señalamos cuando abordamos la pregunta ¿qué son ecuaciones lineales?. En los hechos, una ecuación es un enunciado matemático que constituye una igualdad, pero se trata de lo que llamamos una igualdad no evidente. ¿Por qué? Porque si bien la expresión a la izquierda del signo igual tiene el mismo valor que la expresión a la derecha, ambas son expresiones algebraicas, donde interviene una o más letras cuyo valor real tratamos de averiguar.Veamos un ejemplo sencillo
7 x + 1 =
22
En concreto ¿cuál es el método a aplicar si queremos resolver o hacer una ecuación? El truco es el siguiente: debes elegir convenientemente una operación que vaya dejando aislada a la x en el primer miembro de la igualdad y aplicarla siempre a los dos miembros de la igualdad. Este último punto es muy importante para sostener la igualdad.
Veamos un paso a paso para el ejemplo anterior:
7 x + 1 =
22
7 x + 1 -1 = 22
-1
que queda como
7 x =
21
7 x / 7 = 21 /
7
x = 3
7 x + 1 = 22
7 (3) + 1 = 22
21 + 1 =
22
22 =
22
ECUACIONES CON FRACCIONES
Cómo resolver ecuaciones con fracciones es muy similar a cómo resolver ecuaciones con enteros, pero debes tener en cuenta una serie de reglas básicas que te permitirán manejar las fracciones sin miedo. Una ecuación es fraccionaria si al menos uno de sus términos tiene denominador, es decir, que tengas aunque sea una incógnita dividida entre un número.

Cómo resolver ecuaciones con fracciones se vuelve mucho más sencillo si suprimes los denominadores y la conviertes en una ecuación con enteros. Te podrás preguntar cómo se convierte esto, pero es muy sencillo: Lo primero que tienes que hacer para saber cómo resolver ecuaciones con fracciones es suprimir los denominadores, o sea encontrar el mínimo común múltiplo (m.c.m.) de todos los denominadores que tengas en tu ecuación. (El m.c.m. de dos o más expresiones algebraicas es la que tenga el coeficiente numérico más pequeño y el exponente menor, que se puede dividir exactamente entre cada una de las expresiones dadas)
 En el ejemplo de cómo resolver ecuaciones con
fracciones, el m.c.m. entre los denominadores (que son 2, 1 y 4) es 4 porque 4
se puede dividir exactamente entre 2, entre 1 y entre 4, mira
En el ejemplo de cómo resolver ecuaciones con
fracciones, el m.c.m. entre los denominadores (que son 2, 1 y 4) es 4 porque 4
se puede dividir exactamente entre 2, entre 1 y entre 4, mira  Ahora bien, una vez encontrado el m.c.m. de tu
expresión, lo que tienes que hacer para continuar en el cómo resolver ecuaciones
con fracciones es multiplicar toda la ecuación por ese número. (Recuerda que una
ecuación no se altera si haces las mismas
Ahora bien, una vez encontrado el m.c.m. de tu
expresión, lo que tienes que hacer para continuar en el cómo resolver ecuaciones
con fracciones es multiplicar toda la ecuación por ese número. (Recuerda que una
ecuación no se altera si haces las mismas operaciones de los dos lados del signo igual.)
 Y listo, lo que sigue para saber cómo resolver
ecuaciones con fracciones es encontrar el valor de la incógnita de la misma
forma que resolverías
una ecuación con enteros: reduces términos semejantes, despejas la incógnita
y resuelves.
Y listo, lo que sigue para saber cómo resolver
ecuaciones con fracciones es encontrar el valor de la incógnita de la misma
forma que resolverías
una ecuación con enteros: reduces términos semejantes, despejas la incógnita
y resuelves. 
En caso de que te encuentres con un numerador con un polinomio (que tenga más de un término, o sea que tenga alguna suma o resta en la parte de arriba de la fraccion) no cambia nada en el cómo se resuelven ecuaciones con fracciones: se realizan los mismos pasos; ahora verás.

En el ejemplo puedes observar que todos los numeradores son más de un término, pero eso no afecta en nada, tu debes encontrar el m.c.m. de los denominadores: entre los números 1,5, 3 y 6 su m.c.m. es 30, así que multiplicamos toda la ecuación por 30

Y al eliminar todos los denominadores, entonces resolvemos la ecuación de la misma forma como se resuelve una con enteros: despejando la incógnita.

En estos dos ejemplos es muy sencillo saber cuál es el m.c.m., pero para el caso de que te encuentres con denominadores más complejos, te explico una manera sencilla de encontrar el m.c.m. de cualquier combinación de números, siempre y cuando sean monomios.
- Se descomponen los coeficientes de cada número dado en factores primos (o sea los número que solo pueden dividirse entre sí mismos y entre 1, como 1, 2, 3, 5, 7, 11, 13,17,19,23..) elevados a un cierto exponente.
- Tomamos todas las literales que existen en al menos un término dado con el mayor exponente encontrado.
- Tomamos todos los números primos encontrados con el exponente mayor encontrado.



Por lo tanto el m.c.m. es
ECUACIONES CON RADICALES
Para resolver las Ecuaciones con Radicales, nos apoyamos en la siguiente propiedad: “Cualquier raíz de una ecuación dada, puede ser también raíz de otra ecuación que se obtenga al igualar los cuadrados de los dos miembros de la ecuación propuesta”, sin embargo, al elevar al cuadrado los dos miembros de una ecuación, se obtienen valores para la incógnita, que pueden resultar incorrectos para la ecuación original; estos valores se denominan, Raíces Extrañas de la Ecuación, esto sucede porque los radicales de índice con número par, presentan problemas de indefinición con sub radicales negativos.
Ecuaciones con radicales:
Lo primero que debemos tener en cuenta es el orden de los pasos que necesitamos para resolver una ecuación que contiene radicales:1. Se deja en uno de los miembros un sólo radical, trasladando al otro miembro los demás términos.
2. Los mienbros de la ecuación obtenida se elevan al cuadrado, al cubo, etcétera, y se igualan entre sí dependiendo del índice de la raíz involucrada.
3. Si la ecuación que obtengas no contiene radicales la podemos resolver normalmente, si por el contrario, contiene uno o más radicales se repiten los pasos 1 y 2 hasta que obtengas una ecuación sin radicales, y luego resuelves esta última ecuación.
4. Ahora es necesario que sustituyas los valores obtenidos en el paso anterior, en la ecuación original y ya puedes determinar las raíces extrañas.
El proceso de liberar la ecuación de radicales lo conocemos con el nombre de racionalización de la ecuación.
En los siguientes ejemplos puedes encontrar diferentes formas de solucionar las ecuaciones con radicales:
Primer ejemplo:
√ (x + 3) = 4

Al sustituir x=13 en la ecuación original para revisar si es una raíz extraña o no, nos percatamos que =4, es correcta. Por tanto. S = {13 }.
Segundo ejemplo:
√(2x²-1) =x

Si sustituimos x= -1 en la ecuación original, obtenemos: √2(-1)²-1= (-1)
Podemos observar que el miembro derecho no puede ser negativo, es decir; =-1, por esta razón, descartamos -1 por ser una raíz extraña y ubicamos x=1, entonces tenemos S = {1}.
Tercer ejemplo:
√(4x²-15) -2x = -1
Al sustituir el x=4 en la ecuación
original se tiene:
√(4.42-15)- 2 . 4 = -1√(4.16-15)- 8 = -1
√(64-15)- 8 = -1
√(49)- 8 = -1
7-8=-1.
Esta solución es la correcta y se toma como: S = {4}.
Recuerda seguir practicando operaciones con números radicales, próximamente tendremos nuevos artículos con ejemplos y ejercicios sobre el tema para que puedas seguir profundizando tus conocimientos
LECCIÓN 7. POLINOMIOS
Un polinomio es así:
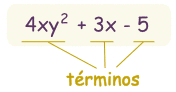 |
| un ejemplo de polinomio este tiene 3 términos |
Están hechos de:
| constantes (como 3, -20, o ½) | |
| variables (como x e y) | |
| exponentes (como el 2 en y2) pero sólo pueden ser 0, 1, 2, 3, ... etc |
Que se pueden combinar usando:
| + - × | sumas, restas y multiplicaciones... |
Estas reglas hacen que los polinomios sean simples, ¡así es
fácil trabajar con ellos!
¿Son polinomios o no?
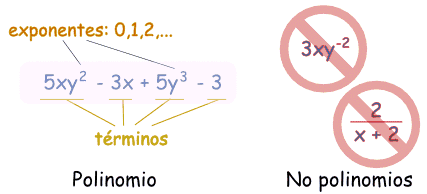
- 3x
- x - 2
- 3xyz + 3xy2z - 0.1xz - 200y + 0.5
- 2/(x+2) no lo es, porque dividir no está permitido
- 3xy-2 no lo es, porque un exponente es "-2" (los exponentes sólo pueden ser 0,1,2,...)
- x/2 está permitido, porque también es (½)x (la constante es ½, o 0.5)
- también 3x/8 por la misma razón (la constante es 3/8, o 0.375)
Monomios, binomios, trinomios
Hay nombres especiales para los polinomios con 1, 2 o 3 términos: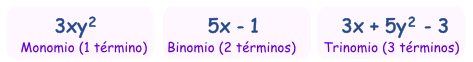
| ¿Cómo te aprendes los nombres? ¡Piensa en bicicletas! |
 |
Muchos términos
Los polinomios pueden tener montones de términos, pero no infinitos términos.¿Qué tienen de especial los polinomios?
Por su definición tan estricta, es fácil trabajar con polinomios.Por ejemplo sabemos que:
- Si sumas o restas polinomios te sale un polinomio
- Si multiplicas polinomios te sale un polinomio
Grado
El grado de un polinomio con una sola variable es el mayor exponente de esa variable.Ejemplo:
| El grado es 3 (el mayor exponente de x) |
septiembre 11/2014
LECCIÓN 6. EXPONENTES FRACCIONARIOS
También se llaman "radicales"
Exponentes
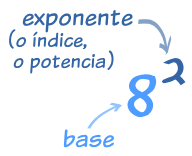 |
El exponente de un número dice cuántas veces se multiplica el
número.
En este ejemplo: 82 = 8 × 8 = 64
|
Exponentes fraccionarios: ½
En el ejemplo de arriba, el exponente es "2", ¿pero y si fuera "½"? ¿Cómo funcionaría?Pregunta: ¿Qué es x½ ?
Respuesta: x½ = la raíz cuadrada de x (o sea x½ = √x)¿Por qué?
Porque si calculas el cuadrado de
x½ tienes: (x½)2 = x1 = x
Para entenderlo, sigue esta explicación de dos pasos:| 1 | Primero, hay una regla general: (xm)n =
xm×n (Porque primero multiplicas x "m" veces, después tienes que hacer eso "n" veces, en total m×n veces) Ejemplo: (x2)3 = (xx)3 = (xx)(xx)(xx) = xxxxxx = x6
Así que (x2)3 = x2×3 =
x6
|
| 2 | Ahora, vemos qué pasa cuando hacemos el cuadrado de
x½:(x½)2 = x½×2 = x1 = xCuando hacemos el cuadrado de x½ sale x, así x½ tiene que ser la raíz cuadrada de x |
Probamos con otra fracción
Vamos a probar otra vez, pero con un exponente de un cuarto (1/4):¿Qué es x¼?
(x¼)4 = x¼×4 = x1 = xEntonces, ¿qué valor se puede multiplicar 4 veces para tener x? Respuesta: La raíz cuarta de x.
Así que x¼ = la raíz cuarta de x
Regla general
De hecho podemos hacer una regla general:
|
Ejemplo: ¿Cuánto es 271/3 ?
Respuesta: 271/3 =¿Qué pasa con fracciones más complicadas?
Las fracciones más complicadas se pueden separar en dos partes:
Así que tenemos esto:
- una parte con un número entero, y
- una parte con una fracción del tipo 1/n
|
Ejemplo: ¿Cuánto es 43/2 ?
Respuesta: 43/2 = 43×(1/2) = √(43) = √(4×4×4) = √(64) = 8|
|
Agosto 26/2014
LECCIÓN 5. EXPONENTES NEGATIVOS
A los exponentes
también se los llama índices.
 |
El exponente de un número nos dice cuántas veces debemos usar ese
número en una multiplicación.
En este ejemplo: 82 = 8 × 8 = 64
|
Entonces, en general:
| an te dice que multipliques a por sí misma un número n de veces: | 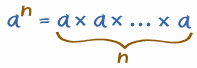 |
8-2
Este exponente es negativo ... ¿qué quiere decir?
Exponentes Negativos
¿Negativo? ¿Qué puede ser lo opuesto a multiplicar? ¡Dividir!La división es la inversa (opuesta) de la multiplicación.Un exponente negativo nos indica cuántas veces dividir por ese número.
Por ejemplo: 8-1 = 1 ÷ 8 = 1/8 =
0,125
Por ejemplo: 5-3 = 1 ÷ 5 ÷ 5 ÷ 5 =
0,008
Pero se puede hacer de una forma más fácil:
5-3 también podría calcularse así:
1 ÷ (5 × 5 × 5) = 1/53 = 1/125
= 0,008
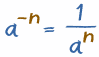 |
El ultimo ejemplo nos mostró una forma más simple de manejar exponentes negativos:
|
Para cambiar el signo (más a menos, o menos
a más) de el exponente usa el Recíproco
(es decir, 1/an)
Entonces, ¿cómo sería 8-2 ?
Por ejemplo: 8-2 = 1 ÷ 8 ÷ 8 = 1/82 =
1/64 = 0,015625
Más ejemplos:
| Exponente negativo | Inversa de un exponente positivo | Respuesta | ||
|---|---|---|---|---|
| 4-2 | = | 1 / 42 | = | 1/16 = 0,0625 |
| 10-3 | = | 1 / 103 | = | 1/1.000 = 0,001 |
Todo Tiene Sentido
Mi método favorito es comenzar con “1” y luego multiplicar o dividir tantas veces como el exponente me diga. Así obtendrás la respuesta correcta, por ejemplo:| Ejemplo: Exponentes de 5 | |||
|---|---|---|---|
| .. etc.. |  | ||
| 52 | 1 × 5 × 5 | 25 | |
| 51 | 1 × 5 | 5 | |
| 50 | 1 | 1 | |
| 5-1 | 1 ÷ 5 | 0,2 | |
| 5-2 | 1 ÷ 5 ÷ 5 | 0,04 | |
| ... etc... | |||
Agosto 20/2014
LECCIÓN 4. LEYES DE LOS EXPONENTES
Los exponentes también se llaman potencias o índices
 |
El exponente de un número dice cuántas veces se multiplica el
número.
En este ejemplo: 82 = 8 × 8 = 64
|
Todo lo que necesitas saber...
Todas las "Leyes de los Exponentes" (o también "reglas de los exponentes") vienen de tres ideas:| El exponente de un número dice multiplica el número por sí mismo tantas veces | |||
| Lo contrario de multiplicar es dividir, así que un exponente negativo significa dividir | |||
|
Si entiendes esto, ¡entonces entiendes todos los
exponentes!
Y todas las reglas que siguen se basan en esas ideas.
Leyes de los exponentes
Aquí están las leyes (las explicaciones están después):| Ley | Ejemplo |
|---|---|
| x1 = x | 61 = 6 |
| x0 = 1 | 70 = 1 |
| x-1 = 1/x | 4-1 = 1/4 |
| xmxn = xm+n | x2x3 = x2+3 = x5 |
| xm/xn = xm-n | x4/x2 = x4-2 = x2 |
| (xm)n = xmn | (x2)3 = x2×3 = x6 |
| (xy)n = xnyn | (xy)3 = x3y3 |
| (x/y)n = xn/yn | (x/y)2 = x2 / y2 |
| x-n = 1/xn | x-3 = 1/x3 |
Explicaciones de las leyes
Las tres primeras leyes (x1 = x, x0 = 1 y x-1 = 1/x) son sólo parte de la sucesión natural de exponentes. Mira este ejemplo:| Ejemplo: potencias de 5 | |||
|---|---|---|---|
| ... etc... |  | ||
| 52 | 1 × 5 × 5 | 25 | |
| 51 | 1 × 5 | 5 | |
| 50 | 1 | 1 | |
| 5-1 | 1 ÷ 5 | 0,2 | |
| 5-2 | 1 ÷ 5 ÷ 5 | 0,04 | |
| ... etc... | |||
La ley que dice que xmxn = xm+n
En xmxn, ¿cuántas veces multiplicas
"x"? Respuesta: primero "m" veces, despuésotras "n" veces, en
total "m+n" veces.
Ejemplo: x2x3 = (xx) × (xxx) = xxxxx = x5
Así que x2x3 = x(2+3) =
x5
La ley que dice que xm/xn = xm-n
Como en el ejemplo anterior, ¿cuántas veces multiplicas "x"? Respuesta: "m" veces, después reduce eso "n" veces (porque estás dividiendo), en total "m-n" veces.
Ejemplo: x4-2 = x4/x2 = (xxxx) / (xx) = xx = x2
(Recuerda que x/x = 1, así que cada vez que hay una x "sobre
la línea" y una "bajo la línea" puedes cancelarlas.)
Esta ley también te muestra por qué x0=1 :Ejemplo: x2/x2 = x2-2 = x0 =1
La ley que dice que (xm)n = xmn
Primero multiplicas x "m" veces. Después tienes que hacer
eso "n" veces, en total m×n veces.
Ejemplo: (x3)4 = (xxx)4 = (xxx)(xxx)(xxx)(xxx) = xxxxxxxxxxxx = x12
Así que (x3)4 = x3×4 =
x12
La ley que dice que (xy)n = xnyn
Para ver cómo funciona, sólo piensa en ordenar las "x"s y las "y"s como en este ejemplo:
Ejemplo: (xy)3 = (xy)(xy)(xy) = xyxyxy = xxxyyy = (xxx)(yyy) = x3y3
La ley que dice que (x/y)n = xn/yn
Parecido al ejemplo anterior, sólo ordena las "x"s y las "y"s
Ejemplo: (x/y)3 = (x/y)(x/y)(x/y) = (xxx)/(yyy) = x3/y3
La ley que dice que 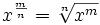
Para entenderlo, sólo recuerda de las fracciones que n/m = n
× (1/m):
Ejemplo: 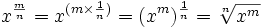
Y eso es todo
Si te cuesta recordar todas las leyes, acuérdate de esto: siempre puedes calcular todo si entiendes las tres ideas de la parte de arriba de esta página.
Ah, una cosa más... ¿Qué pasa si x= 0?
| Exponente positivo (n>0) | 0n = 0 |
| Exponente negativo (n<0) | ¡No definido! (Porque dividimos entre 0) |
| Exponente = 0 | Ummm ... ¡lee más abajo! |
El extraño caso de 00
Hay dos argumentos diferentes sobre el valor correcto. 00 podría ser 1, o quizás 0, así que alguna gente dice que es "indeterminado":| x0 = 1, así que ... | 00 = 1 | |
| 0n = 0, así que ... | 00 = 0 | |
| Cuando dudes... | 00 = "indeterminado" |
Agosto16/2014
LECCIÓN 3: DEFINICIONES BÁSICAS
Qué es una ecuación
Una ecuación dice que dos cosas son iguales. Tendrá un signo de igualdad "=", por ejemplo:| x | + | 2 | = | 6 |
Así que una ecuación es como una afirmación "esto es igual a aquello"
Partes de una ecuación
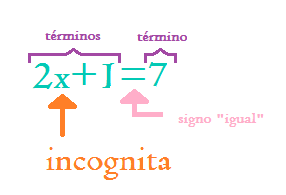
Para que la gente pueda hablar de ecuaciones, hay nombres para las diferentes partes (¡mejor que decir "esta cosa de aquí"!)Aquí tienes una ecuación que dice 4x-7 es igual a 5, y todas sus partes:
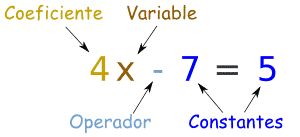 |
Una variable es un símbolo para un número que todavía no conocemos.
Normalmente es una letra como x o y. Un número solo se llama una constante. Un coeficiente es un número que está multiplicando a una variable (4x significa 4 por x, así que 4 es un coeficiente) Un operador es un símbolo (como +, ×, etc) que representa una operación (es decir, algo que quieres hacer con los valores). |
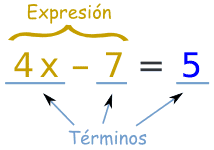 |
Un término es o bien un número o variable solo, o números y variables
multiplicados juntos. Una expresión es un grupo de términos (los términos están separados por signos + o -) |
¡Exponente!
 |
El exponente (como el 2 en
x2) dice cuántas veces usar el valor en una
multiplicación.
Ejemplos:
82 = 8 × 8 = 64
y3 = y × y × y
y2z = y × y × z
|
Ejemplo: y4z2 es más fácil que y × y × y × y
× z × z, o incluso yyyyzz
Polinomio
Un ejemplo de un polinomio: 3x2 + x - 2
Un polinomio puede tener constantes,
variables y los exponentes 0,1,2,3,... Y se puede combinar haciendo sumas, restas y multiplicaciones... ¡pero no divisiones!

Monomio, binomio, trinomio
Hay nombres especiales para polinomios con 1, 2 o 3 términos: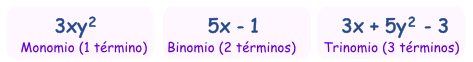
Términos similares
"Términos similares" son términos cuyas variables (y sus exponentes como el 2 en x2) son los mismos.En otras palabras, términos que "se parecen". (Nota: los coeficientes pueden ser distintos)
Ejemplos:
| Términos | Por qué son "similares" | |||
|---|---|---|---|---|
| 7x | x | -2x | porque las variables son todas x | |
| (1/3)xy2 | -2xy2 | 6xy2 | porque las variables son todas xy2 | |
Ejemplo: 7x + x = 8x
Términos no similares
Si no son términos similares, simplemente se les llama "términos no similares":| Términos | Por qué no son "similares" | |||
|---|---|---|---|---|
| -3xy | -3y | 12y2 | ← estos son términos no similares
(xy, y e y2 son todos diferentes) | |
Agosto15/2014
LECCIÓN 2. EXPONENTES
Los exponentes también se llaman potencias o índices
 |
El exponente de un número nos dice cuántas veces se usa el
número en una multiplicación.
En este ejemplo: 82 = 8 × 8 = 64
|
Ejemplo: 53 = 5 × 5 × 5 = 125
- En palabras: 53 se puede leer "5 a la tercera potencia", "5 a la potencia 3" o simplemente "5 al cubo"
Ejemplo: 24 = 2 × 2 × 2 × 2 = 16
- En palabras: 24 se puede leer "2 a la cuarta potencia" or "2 a la potencia 4" o simplemente "2 a la cuarta"
Ejemplo: 96 es más fácil de escribir y leer que 9 × 9 ×
9 × 9 × 9 × 9
Puedes multiplicar cualquier número por sí mismo
tantas veces como quieras con esta notación.
Así que, en general:
| an te dice que multipliques
a por sí mismo, y hay n de esos a's: |
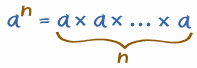 |
Exponentes negativos
¿Negativos? ¿Qué es lo contrario de multiplicar? ¡Dividir! Un exponente negativo significa cuántas veces se divide entre el número.
Ejemplo: 8-1 = 1 ÷ 8 = 0,125
Ejemplo: 5-3 = 1 ÷ 5 ÷ 5 ÷ 5 = 0,008
5-3 también se podría calcular así:
1 ÷ (5 × 5 × 5) = 1/53 = 1/125
= 0,008
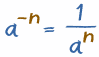 |
Este último ejemplo nos muestra una manera más fácil de manejar exponentes
negativos:
|
| Exponente negativo | Recíproco del exponente positivo | Respuesta | ||
|---|---|---|---|---|
| 4-2 | = | 1 / 42 | = | 1/16 = 0,0625 |
| 10-3 | = | 1 / 103 | = | 1/1.000 = 0,001 |
¿Qué pasa si el exponente es 1 o 0?
Si el exponente es 1, entonces tienes el número solo (por ejemplo 91 = 9)Si el exponente es 0, la respuesta es 1 (por ejemplo 90 = 1)
Tiene sentido
Mi método favorito es empezar con "1" y multiplicar y o dividir tantas veces como diga el exponente, y tendrás la respuesta correcta, por ejemplo:| Ejemplo: potencias de 5 | |||
|---|---|---|---|
| ... etc... |  | ||
| 52 | 1 × 5 × 5 | 25 | |
| 51 | 1 × 5 | 5 | |
| 50 | 1 | 1 | |
| 5-1 | 1 ÷ 5 | 0,2 | |
| 5-2 | 1 ÷ 5 ÷ 5 | 0,04 | |
| ... etc... | |||
Exponentes Negativos
A los exponentes
también se los llama índices.
 |
El exponente de un número nos dice cuántas veces debemos usar ese
número en una multiplicación.
En este ejemplo: 82 = 8 × 8 = 64
|
Entonces, en general:
| an te dice que multipliques a por sí misma un número n de veces: | 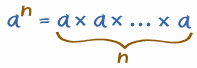 |
8-2
Este exponente es negativo ... ¿qué quiere decir?
Exponentes Negativos
¿Negativo? ¿Qué puede ser lo opuesto a multiplicar? ¡Dividir!La división es la inversa (opuesta) de la multiplicación.
Un exponente negativo nos indica cuántas veces dividir por ese número.
Por ejemplo: 8-1 = 1 ÷ 8 = 1/8 =
0,125
Por ejemplo: 5-3 = 1 ÷ 5 ÷ 5 ÷ 5 =
0,008
5-3 también podría calcularse así:
1 ÷ (5 × 5 × 5) = 1/53 = 1/125
= 0,008
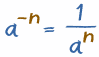 |
El ultimo ejemplo nos mostró una forma más simple de manejar exponentes
negativos:
|
Para cambiar el signo (más a menos, o menos
a más) de el exponente usa el Recíproco
(es decir, 1/an)
Entonces, ¿cómo sería 8-2 ?
Por ejemplo: 8-2 = 1 ÷ 8 ÷ 8 = 1/82 =
1/64 = 0,015625
Más ejemplos:
| Exponente negativo | Inversa de un exponente positivo | Respuesta | ||
|---|---|---|---|---|
| 4-2 | = | 1 / 42 | = | 1/16 = 0,0625 |
| 10-3 | = | 1 / 103 | = | 1/1.000 = 0,001 |
Todo Tiene Sentido
Mi método favorito es comenzar con “1” y luego multiplicar o dividir tantas veces como el exponente me diga. Así obtendrás la respuesta correcta, por ejemplo:| Ejemplo: Exponentes de 5 | |||
|---|---|---|---|
| .. etc.. |  | ||
| 52 | 1 × 5 × 5 | 25 | |
| 51 | 1 × 5 | 5 | |
| 50 | 1 | 1 | |
| 5-1 | 1 ÷ 5 | 0,2 | |
| 5-2 | 1 ÷ 5 ÷ 5 | 0,04 | |
| ... etc... | |||
Agosto 8/2014
LECCIÓN 1. LENGUAJE ALGEBRAICO
VEA PRIMERO LOS VÍDEOS DANDO CLIC AQUI:
¿QUÉ ES ELALGEBRA?
ACABA CON LO PROBLEMAS VERBALES
El lenguaje algebraico es la forma matemática de expresar un enunciado formal o verbal de modo de planear un problema para ser resuelto.
Ejemplos. Expresa en lenguaje algebraico los siguientes enunciados formales.
(1) “El doble de un número”, se
representa por 2x.
(2) “Un número aumentado en dos unidades”, se
representa por x+2.
(3) “El cuadrado de un número desconocido”, se
representa por x2.
Escribe en lenguaje algebraico los siguientes enunciados formales:
1.
El antecesor de un
número
2.
El sucesor de un
número
3.
Un número natural par
4.
Un número natural
impar
5.
La suma de dos números
consecutivos
6.
La suma de dos números
pares consecutivos
7.
La suma de dos números
impares consecutivo.
8.
La suma de dos números
9.
La diferencia de dos
números
10. La diferencia positiva de dos números
11. El producto de dos números
12. El producto de la suma de dos números por su diferencia
13. El cuociente de dos números
14. El inverso aditivo de un número
15. El recíproco de un número
16. Un número aumentado en 3 unidades
17. Un número disminuido en 5 unidades
18. El doble de un número
19. El cuádruplo de un número
20. La mitad de un número
21. La tercera parte de un número
22. Los tres cuartos de un número
23. El cuadrado de un número
24. El cubo de un número
25. La raíz cuadrada de un número
26. El cuadrado del doble de un número
27. El cuadrado de la suma de dos número
28. La suma de los cuadrados de dos números
29. El promedio de dos números
30. La media proporcional de a y b
31. La razón entre de dos números es 2:3
32. La media proporcional entre a y b
33. El producto de dos números es 12
34. El 22% de un número
35. El doble del producto de dos números
36. Un número disminuido en su octava parte
37. El doble de un número aumentado en diez
38. El complemento de un ángulo
Traduzca a enunciado verbal las siguientes expresiones algebraicas:
39. 3(x + y)
40. 3x + y
41. 2(x + y)2
42. (a + b)2 + (a – b)
43. S + S
44. a - 2b
45. 2x2y
Exprese en forma algebraica y reduzca términos si es posible:
46. El perímetro de un rectángulo cuyo lado es 5 unidades más corto que el
otro.
47. Las suma de las áreas de dos cuadrados
de lado a y el antecesor de a.
48. La suma de los volúmenes de dos cubos un de arista (m + n) y (m – n).
Resuelve los siguientes problemas de enunciado verbal.
49. Si al doble de cierto número se suma 6, el resultado es 4 unidades menos
que el triple del número. ¿Cuál es el número?
50. Encontrar el número cuya sexta parte más su novena parte es 15.
51. La suma de tres números naturales consecutivos es 198. ¿Cuáles son dichos
números?
52. La suma de tres números pares consecutivos es 84. ¿Cuáles son dichos
números?


No hay comentarios:
Publicar un comentario