Poliedros
Cuerpos geométricos totalmente limitados por polígonos.

Cuerpos geométricos engendrados por la rotación de una figura plana alrededor de su eje.
Un cuerpo geométrico es una estructura material en la que pueden apreciarse las tres dimensiones: largo, ancho y alto.

Se llama poliedro a todo cuerpo geométrico que esté totalmente limitado por polígonos.
En todo poliedro se distinguen los siguientes elementos:
- Caras: polígonos que limitan el poliedro.
- Aristas: lados de las caras del poliedro.
- Vértices: vértices de las caras del poliedro.
- Ángulos diedros: formados por cada dos caras del poliedro que tengan una arista en común.
- Ángulos poliedros: formados por tres o más caras del poliedro con un vértice común.
- Diagonales: segmentos que unen dos vértices no pertenecientes a la misma cara.
Planos diagonales: formados por cuatro vértices de los cuales sólo dos pertenecen a la misma cara.
Los poliedros se denominan según su número de caras:
·
tetraedro
(cuatro caras),
·
pentaedro
(cinco),
·
exaedro
(seis),
·
heptaedro
(siete),
·
octaedro
(ocho),
·
eneaedro
(nueve),
·
decaedro
(diez),
·
endecaedro (once),
·
dodecaedro (doce),
·
pentadecaedro
(quince)
·
icosaedro
(veinte).
Los demás poliedros no reciben ningún nombre en particular: poliedro de n caras.
Un poliedro es convexo cuando cualquier recta sólo puede cortar a su superficie en dos puntos.
Si alguna recta lo corta en más de dos puntos, el poliedro es cóncavo.
Un poliedro es regular cuando todas sus caras son polígonos regulares iguales entre sí y todos sus ángulos diedros y poliedros son también iguales (sólo existen cinco poliedros regulares).
Si no se cumple alguna de las condiciones anteriores, el poliedro es irregular.
Una superficie poliédrica es un conjunto conexo de polígonos convexos, cada uno de cuyos lados es común a dos polígonos no coplanarios.
Al calificar al conjunto de conexo se significa que dos puntos cualesquiera de la superficie pueden unirse mediante una quebrada cuyos lados pertenecen todos a la propia superficie.
TEOREMA DE EULER
El número de caras de un poliedro más el número de sus vértices
es igual al número de sus aristas más dos.
Dentro de los
poliedros existen tres grupos importantes, que son los prismas, los
paralelepípedos y las pirámides.
El matemático Leonhard Euler nació en Suiza en 1707.
Fue discípulo de Bernoulli, y obtuvo muy pronto la cátedra de
matemáticas de la universidad de Basilea.
En 1730 fue nombrado profesor de la Academia de Ciencias de
San Petersburgo, pasando en 1741, por invitación de Guillermo II, a dirigir la
sección de matemáticas de la
Academia de Berlín.
Ciego desde los 59 años, murió en San Petersburgo en 1783.
PRISMAS

Se denominan prismas aquellos poliedros limitados por dos
polígonos cualesquiera iguales y de lados paralelos llamados bases y por tantos
paralelogramos como lados tienen las bases.
Dichos paralelogramos reciben el nombre de caras laterales del prisma. La
distancia entre las dos bases se llama altura del prisma.
Los lados de las bases constituyen las aristas básicas y los lados de las caras
laterales las aristas laterales, (éstas son iguales y paralelas entre sí).
Sección recta de un prisma es el polígono obtenido al cortar dicho prisma por
un plano perpendicular a las aristas laterales.
Tronco de prisma es la porción de prisma comprendida entre una de las bases y
una sección recta del prisma no paralela a las bases.
Atendiendo al número de caras laterales del prisma, los prismas se clasifican
en:
·
triangulares
(tres caras laterales),
·
cuadrangulares
(cuatro),
·
pentagonales
hexagonales,
(El número de caras laterales depende obviamente
del número de lados de las bases).
Atendiendo a la perpendicularidad entre las bases y las caras laterales del
prisma, un prisma puede ser:
- Recto, cuando las aristas laterales son perpendiculares a las bases (en este caso las caras laterales son rectángulos).
- Oblicuo, cuando no se cumplen las condiciones para que sea recto (en este caso, las caras laterales son rombos o romboides).
Atendiendo a la regularidad de sus bases y el carácter recto u oblicuo del
prisma, los prismas se clasifican en:
- regulares, cuando son rectos y además las bases son polígonos regulares
- irregulares, cuando no son regulares.
Área lateral del prisma es la suma de las áreas de las caras laterales del
mismo.
Cuando se trata de un
prisma recto, es igual al perímetro de la base por la altura del prisma;
Si el prisma es
oblicuo, es igual al perímetro de la sección por la altura del prisma.
1.
Área
total del prisma es igual al área lateral más el área de las bases.
2.
El
volumen del prisma es igual al producto del área de la base por la altura del
prisma.
PARALELEPÍPEDOS
Se denominan paralelepípedos aquellos prismas cuyas bases son paralelogramos. Un paralelepípedo tiene seis caras, paralelas e iguales dos a dos; cuatro diagonales que se cortan en el centro del paralelepípedo y seis planos diagonales.
Entre
los paralelepípedos destacan como más característicos los siguientes:
Cubo
Paralelepípedo
cuyas seis caras son cuadradas (se trata además de un poliedro regular, ya que
todos los ángulos poliedros son también iguales).
Ortoedro
Es
un paralelepípedo cuyas seis caras son
rectángulos (dos de ellas pueden ser cuadradas). También se le conoce con el
nombre de paralelepípedo rectángulo (ya que el cuadrado no es sino un
rectángulo regular, tam-bién puede denominarse al cubo ortoedro regular).
El paralelepípedo recto o rectángulo
es aquél cuyas aristas son perpendiculares a las bases, es decir, cuyos
ángulos diedros son rectos.
El paralelepípedo oblicuo es aquél
cuyas aristas forman con la base un ángulo distinto al recto, es decir, no
son perpendiculares a la base.
|
Romboedro:
Es
un paralelepípedo cuyas seis caras son
rombos o romboides.
Romboedro recto:
Es
un paralelepípedo con cuatro caras
rectangulares y los dos restantes rombos o romboides-
Propiedades de los ortoedros:
- Las cuatro diagonales de un ortoedro son iguales.
- El cuadrado de la diagonal de un ortoedro es igual a la suma de los cuadrados de las tres aristas.
PIRÁMIDES

Se denominan pirámides aquellos poliedros limitados por un polígono cualquiera
llamado base y por tantos triángulos como lados tiene la base que concurren en
un punto, llamado vértice.
Dichos triángulos reciben el nombre de caras laterales de la pirámide.
Las
aristas de la base se llaman aristas básicas y las aristas que concurren en el
vértice, aristas laterales. La distancia entre el vértice y la base es la
altura de la pirámide.
Las pirámides se clasifican:
- Por el número de caras laterales o equivalentemente por el número de lados de la base (la pirámide triangular se denomina tetraedro y todas sus caras son triangulares).
- Por la regularidad de sus elementos: pueden ser regulares, cuando la base es un polígono regular y las caras laterales son triángulos isósceles iguales entre sí, o irregulares, cuando no son regulares.
En toda pirámide regular el pie de la perpendicular desde el vértice a la base,
es decir, el pie de la altura, coincide con el centro de la base.
Se llama apotema de una pirámide regular a la altura de uno cualquiera de los
triángulos laterales.
Si se corta una pirámide por un plano paralelo a la base, resulta un polígono
semejante al que constituye la base (sección paralela a la base) y la razón de
semejanza (cociente entre los lados de los dos polígonos semejantes) es igual a
la razón entre las distancias al vértice de ambos polígonos.
 |
Se
llama tronco de pirámide de bases paralelas a la porción de pirámide
comprendida entre la base y una sección paralela a dicha base.
La
distancia entre las dos bases del tronco es la altura del tronco de pirámide.
Se llama pirámide deficiente a la porción de pirámide comprendida entre el
vértice y la sección paralela a la base.
Si
se trata de una pirámide regular, las caras del tronco son trapecios
isósceles entre sí, y en ese caso se llama apotema del tronco de pirámide a
la altura de una de las caras laterales del tronco de pirámide regular.
|
- El área lateral de una pirámide es igual a la suma de las áreas de las caras laterales de la misma.
- Si la pirámide es regular, su área lateral es igual al semiproducto del perímetro de la base por la apotema de la pirámide.El área total se obtiene sumando el área lateral y el área de la base.
- El área lateral del tronco de pirámide regular de bases paralelas se obtiene efectuando el producto de la semisuma de los perímetros de las dos bases (mayor y menor) por la apotema.
- Sumando al área lateral el área de las bases se obtiene el área total.
- El volumen de la pirámide es igual a un tercio del producto del área de la base por la altura
.
POLIEDROS REGULARES
 |
Tetraedro
regular.
Su
superficie está formada por cuatro caras que son triángulos equiláteros
iguales que se reúnen de tres en tres en cada vértice, es decir, formando
ángulos triedros iguales.
Es
por tanto una pirámide triangular regular.
Tiene
cuatro vértices y cuatro aristas.
|
Hexaedro
regular o cubo.
Su
superficie está constituida por 6 caras que son cuadrados iguales que se
reúnen de tres en tres en cada vértice, formando ángulos triedros iguales.
Es
un prisma cuadrangular regular.
Tiene
8 vértices y 12 aristas.
|
|
Octaedro
regular.
Su
superficie consta de ocho caras que son triángulos equiláteros, agrupados de
cuatro en cuatro en cada vértice formando ángulos tetraedros iguales.
Se
puede considerar formado por la unión de dos pirámides cuadrangulares
regulares, iguales por sus bases.
Tiene
6 vértices y 12 aristas.
|
|
Dodecaedro
regular,
Su
superficie consta de 12 caras que son pentágonos regulares y están agrupadas de
tres en tres formando ángulos triedros iguales.
Tiene
20 vértices y 30 aristas
|
|
Icosaedro
regular.
Su
superficie consta de veinte caras, que son triángulos equiláteros, agrupadas
de cinco en cinco formando ángulos pentaedros iguales.
Tiene
12 vértices y 30 aristas.
|
CUERPOS REDONDOS
CILINDRO
Se llama cilindro de revolución al cuerpo engendrado por un
rectángulo al girar sobre uno de sus lados, tomado como eje de rotación.
Se
produce así un cuerpo limitado por dos círculos iguales denominados bases y una
superficie curva llamada superficie cilíndrica de revolución.
Se denomina generatriz del cilindro al lado del rectángulo que engendra la
superficie lateral del cilindro.
- La distancia entre las dos bases se denomina altura del cilindro y coincide en valor con la generatriz del mismo.
- El área lateral del cilindro se obtiene multiplicando la longitud de la circunferencia de la base por la altura.
- Sumando el área de las bases al área lateral se obtiene el área total del cilindro.
- El volumen del cilindro es igual al producto del área de la base por la altura.
CONO
Se llama cono de revolución al cuerpo engendrado por un triángulo rectángulo que gira sobre uno de sus catetos tomados como eje de rotación.
Se
produce así un cuerpo geométrico limitado por un círculo, denominado base, y
por una superficie curva llamada superficie cónica de revolución.
Cono
|
- Se denomina generatriz del cono a la hipotenusa del triángulo rectángulo que engendra, al girar sobre uno de los catetos, la superficie lateral del cono.
- Vértice del cono es el vértice superior del triángulo generador del mismo.
- Altura del cono es la distancia que hay entre el vértice y la base.
Se denomina tronco de cono de revolución al cuerpo obtenido al cortar un cono
por un plano cualquiera paralelo a la base, restando la parte superior del cono
primitivo, que se denomina cono deficiente.
El tronco de cono consta de dos círculos desiguales denominados bases y de una
superficie lateral troncocónica.
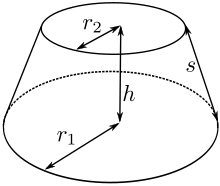 |
Tronco de cono.
|
La altura del tronco de cono de revolución es la distancia entre las dos bases.
También se define el tronco de cono de revolución como el cuerpo engendrado por
un trapecio rectángulo que gira alrededor del lado perpendicular a las bases
tomado como eje de rotación. El lado opuesto se denomina generatriz.
- El área lateral de un cono es igual al semiproducto de la longitud de la base del cono por la generatriz.
- Añadiendo el área de la base al área lateral se obtiene el área total del cono.
- El volumen del cono es igual a un tercio del producto del área de la base por la altura.
ESFERA

Cuerpo geométrico engendrado por la rotación de un
semicírculo que gira alrededor de su diámetro, tomado como eje de revolución.
La superficie que delimita la esfera se llama superficie esférica.
Todos
los puntos de la esfera equidistan de un punto interior denominado centro de la
esfera.
Radio
de una esfera es el segmento que une al centro con un punto cualquiera de la
superficie esférica.
Diámetro
de una esfera es el segmento que une dos puntos cualesquiera de la superficie
esférica, pasando por el centro de la misma.
Las secciones de un plano con una esfera son siempre círculos de tamaño
creciente con la mayor proximidad al centro de la esfera, en donde los círculos
son máximos, por coincidir su radio con el de la esfera.
- El área de la superficie esférica es igual a cuatro veces el área de un círculo máximo.
d2 pi
- El volumen de la esfera es igual a cuatro tercios del producto de p por el cubo del radio de la esfera.
D3
pi/6
FIGURAS ESFÉRICAS
| Zona esférica. Porción de superficie esférica delimitada por dos planos secantes paralelos entre sí. Casquete esférico. Es cada una de las porciones en que queda dividida la superficie esférica cuando se corta por un plano secante a la misma (es un caso particular de zona esférica, cuando uno de los dos planos es tangente a la superficie esférica). |
 |
SUPERFICIE CÓNICA DE REVOLUCIÓN
Es
la superficie engendrada por la rotación de una recta alrededor de otra fija,
llamada eje, a la que corta de modo oblicuo.
Todas
las generatrices se cortan en un punto central llamado vértice, que divide en
dos partes (llamadas hojas) a la superficie cónica de revolución.
CÓNICAS
Un
plano que corte a la superficie cónica de revolución puede dar lugar a cuatro
tipos de secciones según las posiciones relativas del plano y la superficie.
Circunferencia.
Es
la sección producida en una superficie cónica de revolución por un plano
perpendicular al eje.
Elipse.
Es
la sección producida en una superficie cónica de revolución por un plano
oblicuo al eje que no sea paralelo a la generatriz y que forme con el mismo
un ángulo mayor que el que forman el eje y la generatriz.
Es
una curva cerrada, lugar geométrico de los puntos de un plano cuyas
distancias a los puntos fijos, llamados focos, dan una suma constante.
|

Distintas
clases de cónicas:
|
Parábola.
Es
la sección producida en una superficie cónica de revolución por un plano que
corta oblicuamente al eje, siendo paralelo a la generatriz.
Se
trata de una curva abierta, lugar geométrico de los puntos de un plano
equidistantes de un punto fijo (foco) y de una recta fija (directriz), que se
prolonga hasta el infinito.
Hipérbola.
Es
la sección producida en una superficie cónica de revolución por un plano que
corta oblicuamente al eje, formando con él un ángulo menor que el que forman
eje y generatriz, por lo que incide en las dos hojas de la superficie cónica.
Es
una curva abierta que se prolonga indefinidamente y consta de dos ramas
separadas.
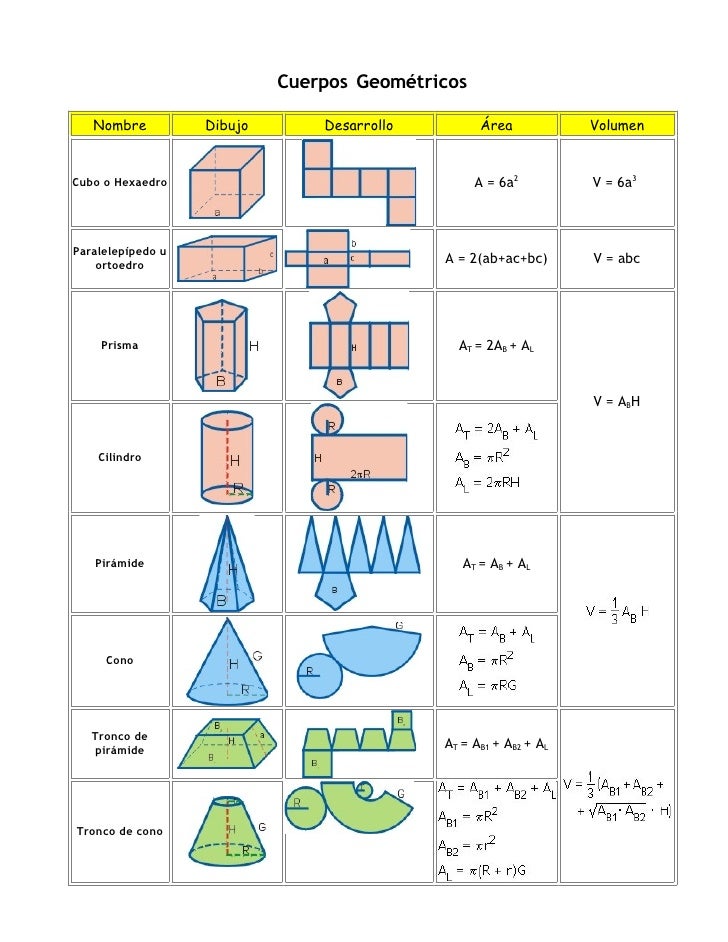
ÁREAS Y VOLÚMENES de CUERPOS GEOMETRICOS

No hay comentarios:
Publicar un comentario